Pythagore

Mathématicien et philosophe grec (Samos vers 570-Métaponte vers 480 avant J.-C.), fondateur d'une école dont l'influence fut considérable en Italie du Sud, puis en Grèce.
1. L'être légendaire

Il n'est guère, dans l'Antiquité, de figure plus mystérieuse, ni qui ait posé de problèmes plus embarrassants aux historiens que celle de Pythagore. Celui-ci passe pour n'avoir rien écrit, et sa pensée ne fut sans doute connue jusqu'à l'époque de Socrate que par une tradition orale, elle-même entourée de secret.
En outre, il est devenu très tôt, peut-être même déjà de son vivant, une figure de légende. On le disait fils d'Apollon ou d'Hermès (le philosophe lui-même l'aurait déclaré), dont il aurait reçu le don de garder le souvenir de ses précédentes réincarnations… On racontait aussi qu'il avait un fémur d'or, qu'il possédait des dons prophétiques et celui d'ubiquité, et qu'il était descendu aux Enfers, où il avait vu l'âme d'Hésiode enchaînée à une colonne de bronze et celle d'Homère suspendue à un arbre et entourée de serpents pour avoir parlé des dieux comme ils l'avaient fait.
Pythagore était-il déjà une énigme pour Aristote, qui évitait le plus souvent de prononcer son nom pour ne parler que de « ceux qu'on appelle pythagoriciens » …
2. Les faits historiques
Il n'en reste pas moins que l'existence de Pythagore est un fait certain. Son père se nommait Mnésarque. On ne sait presque rien de la vie de Pythagore à Samos, sinon qu'il eut probablement pour maîtres Phérécyde et Anaximandre. Ces étranges personnages, à demi légendaires, ne sont pas sans évoquer les chamans orientaux : visionnaires inspirés, mages extatiques, purificateurs et guérisseurs, ils se donnent pour des « hommes divins », médiateurs entre l'homme et le dieu, et s'autorisent d'une faculté exceptionnelle de voyance qui leur permet d'entrer en contact avec l'invisible et de se remémorer leurs existences antérieures.

C'est à cette période, également, qu'on peut rattacher les voyages d'études que Pythagore accomplit en Perse, en Gaule, en Crète, en Égypte. Revenu à Samos, il trouva sa patrie sous le joug de Polycrate et la quitta, à quarante ans, pour l'Italie, où, à Crotone, en Grande-Grèce, il fonda une école qui ne tarda pas à prendre un grand développement et vers laquelle affluaient un nombre considérable de disciples, lucaniens, messapiens et romains.
3. La secte religieuse
Ces disciples formaient autour du maître une espèce de confraternité dont le but était mystique et, par la suite, politique, plus que philosophique. La tradition a surtout retenu le mysticisme et représente les pythagoriciens comme des hommes tout de blanc vêtus, qui fuient le contact des femmes en couches, évitent d'entrer dans la maison d'un mort, refusent énergiquement de croquer une fève ou de manger un œuf… Bref, leur existence quotidienne paraît encombrée de tabous et d'interdictions en tout genre, tandis que sur leur vie communautaire plane le mystère : les femmes furent admises dans le groupe, telle Théano, épouse et disciple de Pythagore ; tous les membres de la communauté devaient, avant de paraître devant le maître, observer une période de silence qui durait cinq ans ; ils étaient tenus, en outre, à garder le secret le plus absolu sur les doctrines enseignées, et l'autorité du maître, qui se considérait comme le seul dépositaire de la vérité, était souveraine.
4. L'enseignement au sein de la société

Cette société était divisée en deux classes. Les « auditeurs » étaient tenus au silence et ne pouvaient que retenir les paroles du maître. Les « mathématiciens », c'est-à-dire les « instruits », étant passés par une longue période de préparation, pouvaient poser des questions et émettre des opinions. L'enseignement de Pythagore était réservé à un petit nombre, les autres recevant donc une parole souvent déformée. Là où les premiers pouvaient ne percevoir que des propos à valeur symbolique, les derniers voyaient des instructions à respecter à la lettre malgré leur absence de signification. On ignore par exemple pourquoi la consommation des fèves était interdite. De manière générale, les comportements étaient soumis à des obligations nombreuses.
5. L'hétairie politique
Par la suite, l'école pythagoricienne de Crotone devint une hétairie politique de tendance aristocratique, qui connut un grand succès à Crotone et eut de nombreuses ramifications à Sybaris, à Rhêgion (aujourd'hui Reggio) et en Sicile. C'est sous cet aspect qu'elle provoqua de la part des démocrates de vives réactions, qui devaient aboutir à l'incendie de l'édifice où tous les pythagoriciens se trouvaient ; tous, sauf deux, y perdirent la vie, y compris Pythagore. Suivant une autre tradition, ce dernier serait parvenu à s'échapper, mais aurait péri pour s'être refusé à traverser un champ de fèves, plantes que la secte tenait pour sacrées.
Selon d'autres théories, l'opposition des démocrates contraignit Pythagore à quitter Crotone. Vers 500 av. J.–C., il s'installa à Métaponte, où il passa le reste de sa vie. Les révolutions démocratiques du milieu du Ve s. achevèrent de détruire la secte, chassant les derniers disciples vers Tarente.
Vue sous l'angle politique, l'éducation collective des pythagoriciens apparaît comme un véritable dressage, qui comprenait des repas pris en commun, ou syssities, le compagnonnage (conséquence de la mise en commun des biens), enfin des techniques telles que les exercices physiques, l'apprentissage de la musique et la réglementation des nourritures. De là, nous sont parvenues certaines traditions militaristes, car, pour les pythagoriciens, il était « noble de mourir à la suite de blessures reçues de face » et il fallait « combattre non en parole, mais en actes, car il est juste et pieux de faire la guerre quand on la fait homme contre homme […] ».
6. La « science » de Pythagore

Cette « science », à laquelle la tradition veut qu'il ait donné, le premier, le nom de philosophie, ne peut être envisagée séparément des buts mystico-politiques de la secte. Accueillant en elle les connaissances les plus diverses (Héraclite accusa Pythagore de « polymathie »), elle accordait vraisemblablement une place importante à ce qui recevra plus tard le nom de mathématiques et qui devait fournir à la fois un accès au divin et le modèle de l'ordre à réaliser par les lois de la cité. L'un des principaux mérites de Pythagore serait, selon Aristoxène, d'avoir « élevé l'arithmétique au-dessus des besoins des marchands ».

De ce qui n'était, chez les Égyptiens, qu'un ensemble de recettes empiriques, établies à des fins utilitaires, Pythagore aurait fait, le premier, une science démonstrative. Mais sa véritable originalité fut, en fait, d'envisager le nombre dans une perspective religieuse et mystique ; et c'est la religion qui, libérant la mathématique de sa visée utilitaire, ouvrit ici la voie à la spéculation abstraite. Il est à peu près certain que remonte à Pythagore lui-même l'affirmation, rapportée par Aristote, selon laquelle toutes choses sont des nombres. Partant peut-être de considérations sur l'accord musical, qui se laisse ramener à une proportion mathématique, Pythagore serait arrivé à l'idée que « les nombres sont pour ainsi dire le principe, la source et la racine de toutes choses ».
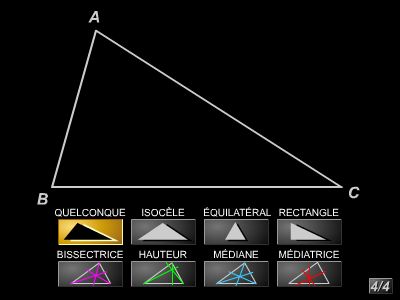
À partir de là s'est développée toute une arithmologie mystique, assignant aux nombres des propriétés qualitatives. Ainsi, la tétraktys, ou somme des quatre premiers nombres, qui est représentée par le triangle décadique et qui enveloppe en elle les natures du pair et de l'impair, sera désignée comme le fondement de toutes choses. De ce type de spéculation relèveraient les découvertes mathématiques que la tradition attribue à Pythagore : outre le théorème qui porte son nom et celui de la somme des angles du triangle, la construction de certains polyèdres réguliers, les débuts du calcul des proportions.
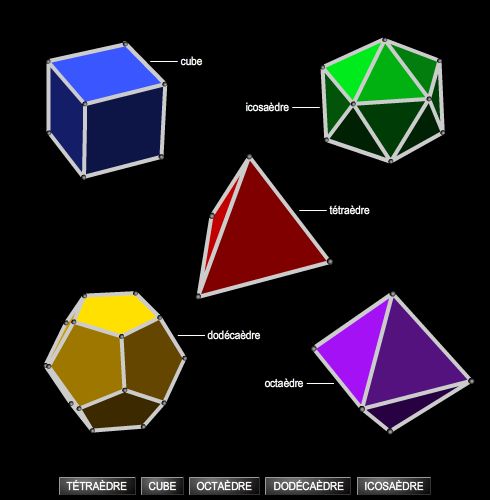
Une telle pensée se devait de concevoir la production du nombre sur le modèle de celle de l'harmonie du nombre : le cosmos serait le résultat de l'aspiration d'un vide illimité, situé hors du ciel et qui, absorbé par celui-ci, y séparerait des unités en instaurant des intervalles (le nombre étant ainsi produit non par addition, mais par la division d'une unité enveloppante). À la source de cette aspiration et de l'agencement des choses qu'elle réalise se trouverait un feu central, ordonnant autour de lui la révolution des corps célestes.
Premier pas en direction d'une vision positive des choses, mais sur lequel il faut bien se garder de projeter la conception moderne de la science, le courant de pensée ouvert par Pythagore apporte un témoignage privilégié de cette mutation, qui s'accomplit en Grèce, d'une pensée religieuse à une pensée rationnelle (pythagorisme).
6.1. L'importance des nombres
Parmi les croyances en cours chez les pythagoriciens figure la métempsycose, c'est-à-dire la transmigration des âmes, doctrine d'origine indienne. Mais le trait le plus original est l'importance accordée au nombre, ou plus exactement au nombre entier. Celui-ci donne lieu à une représentation par des points. Leur éventuel arrangement régulier en figures simples induit la considération de familles de « nombres figurés », les nombres triangulaires (1, 2, 3, 6, etc.) et les nombres carrés (1, 4, 9, etc.) par exemple. Les pythagoriciens développèrent une arithmétique autour de ces considérations.
Ils s'intéressèrent aussi aux nombres « parfaits », ceux qui égalent la somme de leurs facteurs, tel 6 égal à 1 + 2 + 3, et dont Euclide à donné la théorie générale dans le livre IX des Éléments.
Les nombres « amis » constituèrent un autre domaine de recherche. Il s'agit de paires de nombres dans lesquelles la somme des facteurs de l'un égale l'autre. L'exemple de 284 et de 220 aurait été trouvé par Pythagore, et il aurait été le seul connu dans l'Antiquité.
Les proportions furent également un objet d'étude poussée, repris par Euclide, qui en étendit la théorie à toutes sortes de grandeurs dans le livre V des Éléments.
6.2. Arithmétique et cosmologie
La raison de cet intérêt prononcé pour l'arithmétique réside dans la conviction que les nombres constituent l'essence des choses. Cette doctrine tirait sans doute sa source de trois considérations. L'une fut la relation constatée entre les hauteurs des sons et les longueurs des cordes des instruments de musique. Une autre fut peut-être le constat qu'un triangle dont les côtés ont pour mesures 3, 4 et 5 est rectangle. La troisième fut l'existence de relations numériques dans les mouvements des corps célestes.
6.3. Le théorème de Pythagore
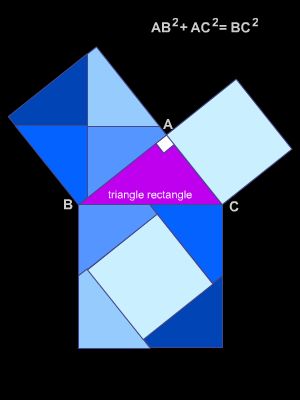
Les recherches géométriques furent moins développées par les pythagoriciens. Le « théorème de Pythagore » ne fut ni découvert ni sans doute démontré par celui qui lui a donné son nom. Ces recherches conduisirent néanmoins à une découverte de l'incommensurabilité, de première importance pour le développement des mathématiques. La diagonale du carré ne contenant pas un nombre entier de fois le côté, le problème était de trouver une fraction du côté qui soit contenue un nombre entier de fois dans l'un et dans l'autre. Des pythagoriciens démontrèrent l'impossibilité de trouver une telle « commune mesure », jetant un trouble profond dans les cercles savants de la société.
L'énoncé du théorème : le carré de l'hypoténuse (c) d'un triangle rectangle est égal à la somme des carrés des deux autres côtés (a, b) :
c2 = a2 + b2.
Pour en savoir plus, voir l'article théorème de Pythagore.
6.4. Astres et musique
Les pythagoriciens cultivèrent par ailleurs la théorie des intervalles musicaux ainsi que l'étude des astres. Ils furent les premiers à classer les planètes, c'est-à-dire, outre le Soleil et la Lune, Mercure, Vénus, Mars, Jupiter et Saturne, selon leurs distances supposées à la Terre. Ils tentèrent d'accorder ces distances, ainsi que les périodes de révolutions, avec les intervalles musicaux, développant la conception des sphères célestes et de leur musique.