nombre

(latin numerus)

Notion qui permet de compter, de dénombrer les choses ou les êtres, de classer les objets, de mesurer les grandeurs.

MATHÉMATIQUES

Les nombres sont l'une des plus étonnantes inventions de l'intelligence humaine et ce de plusieurs points de vue. Psychologique tout d'abord, le fait de savoir compter suppose un processus d'abstraction qui ne se forme que lentement. Historique ensuite, il a fallu de nombreux essais et un temps très long pour que se mette en place un système de numération efficace. Philosophique enfin, le dénombrement pose en effet le problème de la pluralité et de l'identité.

Les principes de la numération

L'idée de compter par « paquets » est venue assez tôt ; on a commencé par construire des symboles nouveaux pour chacun des « niveaux » : 10, 100, 1 000, etc. C'est le cas des écritures égyptienne, grecque ou romaine. Ce mode de représentation conduisait à une impasse : on ne pouvait écrire un grand nombre qu'à condition d'avoir le symbole correspondant. De plus, tous les systèmes ne formaient pas les « paquets » de la même manière : certains changeaient de « niveau », par exemple, à 10, d'autres à 12 ou à 60. On trouve un reste de ces pratiques dans les actuelles mesures de temps et d'angles. La grande découverte qui donna naissance à l'actuel système d'écriture des nombres vient probablement de l'Inde, véhiculée et transformée par les Arabes. C'est une écriture de position dans laquelle les symboles sont peu nombreux. La place de chacun d'entre eux dans le nombre en indique le « niveau ». On peut donc, grâce à ce système, écrire potentiellement n'importe quel nombre à condition d'avoir (et de créer) un signe pour marquer l'absence, le zéro.

La théorie des nombres

Les nombres entiers constituent la base sur laquelle repose l'édifice mathématique. C'est par extensions successives des opérations sur les entiers que l'on définit tous les autres nombres. Ils servent, à leur tour, à définir la continuité des points d'une droite et sont à l'origine de la théorie des fonctions. Enfin, ces fonctions permettent, par la géométrie analytique, de traduire en équations tout problème sur les figures de l'espace. Cela explique la place centrale qu'occupe, en mathématiques, l'arithmétique, ou théorie des nombres. D'un point de vue logique, la consistance, c'est-à-dire la non-contradiction, de celle-ci suffit à garantir la validité de l'ensemble des mathématiques.

Les ensembles de nombres

Les nombres entiers

Ils forment une échelle commençant par un point de départ, le zéro dans les systèmes usuels, et se poursuivant indéfiniment. Cette échelle indique, d'une part, un ordre : premier, deuxième, troisième…, d'autre part, une grandeur : un, deux, trois… À cette dernière fonction, dite « cardinale », est liée, celle d'opération (addition et multiplication). La somme et le produit de deux entiers sont encore des entiers. On peut définir leurs opérations réciproques (ou inverses), la soustraction et la division. Toutefois, dans l'ensemble ℕ des nombres entiers, ces dernières ne sont pas toujours possibles. On peut calculer 7 − 5 mais non 5 − 7 ; de même, on peut diviser 12 par 4 mais non par 5. Pour surmonter cette difficulté, on a étendu ℕ aux nombres relatifs puis aux nombres rationnels, de manière à rendre les calculs toujours réalisables.

Les nombres relatifs

Pour donner un sens à une soustraction comme 5 − 7, impossible pour les entiers, on prolonge ceux-ci par une suite symétrique par rapport à 0 ; celle-ci est formée des mêmes nombres précédés du signe moins et inscrits dans un ordre inverse. L'ensemble s'écrit alors : {… − 4, − 3, − 2, − 1, 0, 1, 2, 3, 4 …}. Ce nouvel ensemble ℤ des entiers relatifs s'étend indéfiniment dans les deux sens ; il est formé de deux parties, les nombres négatifs, précédés du signe moins, et les nombres positifs.

Les nombres rationnels

Une division de A par B n'est possible, avec les entiers, que si A est un multiple de B. Quand ce n'est pas le cas, la méthode d'extension, qui a servi pour les soustractions, amène à poser ce quotient comme une entité nouvelle définie précisément par la division : le quotient de 2 par 3, par exemple, est un rationnel a. Pour que cette définition soit pleinement opératoire, il faut indiquer quels sont les critères d'égalité entre ces nouveaux nombres et comment on peut effectuer des opérations avec eux. Leur représentation se fait de deux façons : soit sous la forme de fraction (a s'écrit alors 2/3), soit sous la forme décimale (a est alors égal à 0,666…).

On a précédemment construit une suite de trois ensembles, celui des entiers ℕ, son extension aux relatifs ℤ et, enfin, l'extension de ce dernier aux rationnels ℚ. Avec ℚ est réalisée la clôture algébrique de l'ensemble des entiers par rapport aux quatre opérations qui y sont naturellement définies. En effet, l'ensemble des nombres rationnels est le plus petit ensemble contenant les entiers et dans lequel toutes les opérations définies sur ℕ ainsi que leurs inverses sont possibles sans aucune restriction.

Les nombres réels

Dès l'Antiquité grecque, on a découvert que certaines grandeurs issues de constructions géométriques (par exemple 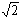ou π) échappent à toute détermination exacte : ce sont les nombres irrationnels. Parmi ceux-ci, certains, dits « nombres algébriques », peuvent être décrits comme solutions d'une équation algébrique à coefficients rationnels ; d'autres, dits « nombres transcendants » (tel π), ne sont solution d'aucune équation à coefficients rationnels. L'ensemble ℝ des nombres réels est ainsi formé par tous les nombres rationnels et irrationnels.

Les nombres complexes

Dans l'ensemble ℝ ainsi constitué, il reste cependant une opération impossible : le calcul de la racine carrée d'un nombre négatif. Pour dépasser cette impossibilité, on est amené à construire des nombres, dits « imaginaires », tels que le nombre i, vérifiant par définition la relation : i² = − 1. On étend donc ainsi les nombres réels en les plongeant dans un ensemble plus vaste dans lequel on peut extraire les racines de n'importe quel nombre positif ou négatif. L'ensemble obtenu est l'ensemble ℂ des nombres complexes.