lentille
Volume de verre ou d'une substance réfringente quelconque, limité par des surfaces généralement sphériques, utilisé pour former des images optiques.
OPTIQUE
Introduction
Les lentilles sont des objets transparents qui modifient la propagation de la lumière et dévient les rayons lumineux. Les lentilles les plus courantes possèdent une symétrie de révolution autour d'un axe et sont limitées par deux calottes sphériques, ou par une calotte sphérique et un plan. Elles entrent dans la construction d'un grand nombre d'instruments : lunettes, loupes, microscopes, appareils photographiques, caméras, appareils de projection, etc. On en trouve également dans le corps humain : le cristallin de l'œil est une lentille convergente particulière à courbure variable ; son rôle est de faire converger sur la surface de la rétine les rayons lumineux qui pénètrent dans l'œil.
Lentilles et images
On appelle image d'un point A le point A' où se rencontrent, après passage par la lentille, tous les rayons lumineux issus du point A. Lorsque les rayons issus de la lentille se coupent au point A', l'image est dite réelle. Les objectifs d'appareils de photo forment des images réelles : c'est la concentration de lumière à l'emplacement des images réelles qui impressionne la pellicule. Au contraire, lorsque, à la sortie de la lentille, les rayons semblent provenir d'un point A' situé sur le prolongement imaginaire des rayons, on dit que l'image est virtuelle : les loupes, les verres de lunettes forment des images virtuelles, dont le cristallin donne ensuite une image réelle située sur la rétine.
Pour qu'une image soit nette, il faut qu'à un point objet corresponde un point image, et non une tache : le système est alors dit stigmatique. Cela est très difficile à réaliser, et même impossible dans le cas d'objets de grandes dimensions. Cependant, on obtient un résultat satisfaisant lorsque les conditions de Gauss sont satisfaites, c'est-à-dire lorsque les rayons lumineux font un angle faible avec l'axe optique, ainsi qu'avec les normales aux surfaces optiques.
Les différents types de lentilles
Lentilles convergentes et lentilles divergentes
Suivant la forme de leurs faces, on distingue six sortes de lentilles, trois à bords minces (biconvexe, plan-convexe et ménisque à bords minces), et trois à bords épais (biconcave, plan-concave et ménisque à bords épais). Lorsque l'indice de la lentille est plus grand que celui du milieu dans lequel elle se trouve, les lentilles à bords minces sont convergentes, c'est-à-dire qu'elles transforment un faisceau de lumière parallèle en un faisceau convergent vers un point. Inversement, les lentilles à bords épais sont divergentes : elles transforment un faisceau de lumière parallèle en un faisceau divergent.C'est le contraire lorsque la lentille est plongée dans un liquide d'indice plus grand que celui du matériau dont elle est constituée.
Lentilles minces
On qualifie de mince une lentille dont l'épaisseur est faible par rapport aux rayons de courbure de ses faces. Les constructions et les calculs concernant les lentilles minces sont beaucoup plus simples que dans le cas général. On peut les considérer comme une première approximation pour des lentilles modérément épaisses.
Axe optique et centre optique
On appelle axe principal ou axe optique de la lentille la droite qui passe par les centres de courbure de ses faces (l'un des centres est rejeté à l'infini lorsqu'une des faces est plane).
Il existe un point O situé sur l'axe optique qui possède la propriété suivante : à la sortie de la lentille, tout rayon qui est passé par le point O est parallèle à la direction qu'il avait avant de rencontrer la lentille. On appelle le point O le centre optique de la lentille.
Pour les lentilles minces, on peut considérer que les sommets des deux faces de la lentille sont confondus. Le centre optique coïncide, lui aussi, avec ces deux points.
Les foyers d'une lentille
Foyers principaux
On appelle foyer principal image F' d'une lentille le point vers lequel convergent (ou d'où semblent diverger), après passage dans la lentille, tous les rayons lumineux provenant d'un faisceau cylindrique parallèle à l'axe de la lentille.
On appelle foyer principal objet le point F tel que tous les rayons issus de ce point (ou qui convergeraient vers ce point en absence de la lentille) forment, après passage par la lentille, un faisceau cylindrique parallèle à l'axe.
Le foyer est réel si la lumière passe effectivement par ce point. Il est virtuel si ce sont les prolongements imaginaires des rayons qui y passent. Les foyers sont réels pour les lentilles convergentes et virtuels pour les lentilles divergentes.
Plans focaux et foyers secondaires
Le plan perpendiculaire à l'axe et passant par le foyer image F' est le plan focal image P'. On définit de même le plan focal objet P par rapport au foyer objet F.
Un faisceau incident formé de rayons parallèles entre eux mais inclinés par rapport à l'axe optique converge vers un point du plan focal image qui n'est pas situé sur l'axe optique. On appelle ce point H' un foyer secondaire image : dans le cas des lentilles minces, il est situé à l'intersection du plan focal image et du rayon incident qui passe par le centre optique et n'est donc pas dévié en traversant la lentille.
De même, tous les rayons issus d'un point foyer secondaire objet H, situé dans le plan focal objet à l'écart de l'axe optique, forment, après traversée de la lentille, un faisceau parallèle, incliné par rapport à l'axe optique. Pour une lentille mince, la direction de ce faisceau émergeant est celle du rayon HO, qui n'est pas dévié à la traversée de la lentille.
Distance focale et puissance d'une lentille
La position et la taille des images données par une lentille sont déterminées par sa distance focale image f' et sa distance focale objet f qui dépendent des indices de réfraction de la lentille et des milieux extérieurs, de son épaisseur et des rayons de courbure de ses deux faces. Par convention, la distance focale image est positive pour les lentilles convergentes et négative pour les divergentes. Dans les cas où les milieux de part et d'autre de la lentille ont même indice de réfraction, les distances focales f et f' sont opposées.
Dans le cas des lentilles minces, la distance focale image représente la distance entre le centre optique et le foyer image. De même, la distance focale objet représente la distance entre le centre optique et le foyer objet.
Pour une lentille mince d'indice n placée dans l'air dont les faces sont des calottes sphériques de rayons respectifs R1 et R2, la distance focale est donnée par la « formule des lunetiers » : 1/f = (n − 1) (1/R1 − 1/R2).
La puissance P d'une lentille (on dit aussi la convergence) est exprimée en dioptries et définie comme l'inverse de la distance focale mesurée en mètres : P = 1/f. Cette grandeur est positive pour les lentilles convergentes et négative pour les lentilles divergentes. Le système formé par l'association de plusieurs lentilles minces et accolées est analogue à une seule lentille dont la puissance est égale à la somme algébrique des puissances de chacune.
Construction géométrique des images
D'un objet plan, schématisé par un segment AB, la lentille donne une image A'B' dont il est possible de déterminer graphiquement la position et les dimensions (on suppose les conditions de Gauss réalisées même si, pour la commodité du tracé, certains points sont un peu éloignés de l'axe principal).
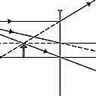
Nous considérerons seulement le cas des lentilles minces. La construction repose sur les constatations suivantes : un rayon lumineux incident parallèle à l'axe est réfracté en direction du foyer image ; un rayon passant par le centre de la lentille n'est pas dévié ; un rayon incident passant par le foyer objet sort de la lentille parallèlement à l'axe optique.
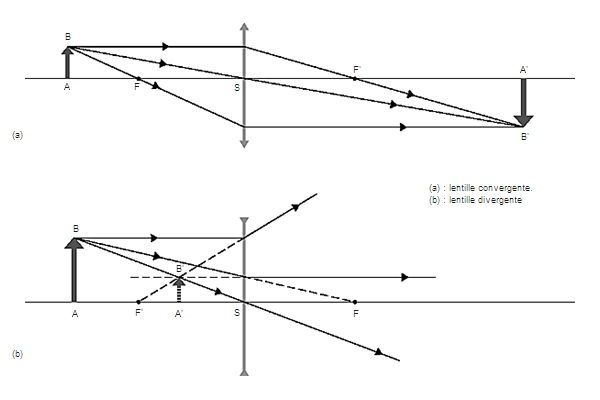
Cas d'une lentille mince divergente
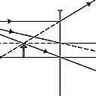
On choisit le point A sur l'axe optique de la lentille et AB perpendiculaire à cet axe. L'image cherchée est un segment A'B', également perpendiculaire à l'axe optique et parfaitement déterminé si l'on connaît l'image B' du point B. Pour construire B', on choisit deux rayons particuliers du faisceau issu de B ; par exemple, on peut utiliser le rayon incident passant par le foyer objet F (qui émerge parallèlement à l'axe optique) et le rayon passant par le centre optique O (qui n'est pas dévié). L'intersection des deux rayons émergents est l'image B' cherchée : tous les rayons passant par B passent par B' après traversée de la lentille. Selon la position de l'objet, l'image est réelle ou virtuelle.
Cas d'une lentille mince convergente
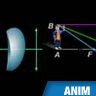
On opère de la même façon que pour les lentilles convergentes : on utilise deux rayons particuliers issus du point B ; l'un passant par O et l'autre par F, par exemple. Le premier n'est pas dévié ; au second correspond un rayon émergent parallèle à l'axe optique. L'intersection de ces deux rayons est le point B' cherché. L'image d'un objet réel est toujours virtuelle.
La relation de conjugaison image - objet
Les formules de conjugaison permettent de trouver la position de l'image d'un objet donné. Si A est un objet situé sur l'axe optique, son image A' est également sur l'axe optique. La formule de Newton donne la position de A' ; elle est valable pour toutes les lentilles immergées dans un milieu unique, aussi bien les lentilles minces que les lentilles épaisses :
F′A′ FA = ff′.
Cette formule est simple et universelle, mais elle nécessite que l'on connaisse la position des foyers. Pour les lentilles minces immergées dans un milieu unique, on peut utiliser une formule dans laquelle les distances sont mesurées à partir du centre optique de la lentille, qui est facile à repérer :
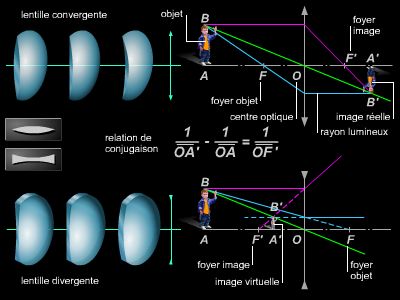
1/OA′ − 1/OA = 1/OF′.
L'expression du grandissement
Si AB est un objet perpendiculaire à l'axe optique, son image A'B' est elle aussi perpendiculaire à l'axe optique. Le grandissement est le quotient de la longueur de l'image par celle de l'objet. Lorsque ce rapport est positif, l'image et l'objet sont de même sens. Lorsque le grandissement est négatif, l'image est à l'envers (si l'on considère que l'objet est à l'endroit). Pour les lentilles minces immergées dans un milieu unique, le grandissement est donné par la formule :
A′B′/AB = OA′/OA
Il est facile de vérifier que, lorsque l'objet et l'image sont tous deux réels, l'image est inversée.
Les aberrations
Lorsque les lentilles sont utilisées en respectant les conditions de Gauss, les images obtenues sont dites approximativement stigmatiques. Mais dans les systèmes centrés, ces conditions ne peuvent pas toujours être respectées ; ils ne donnent alors pas d'images stigmatiques, pas même de façon approchée : ils sont affectés par des aberrations chromatiques ou géométriques.
Les aberrations chromatiques
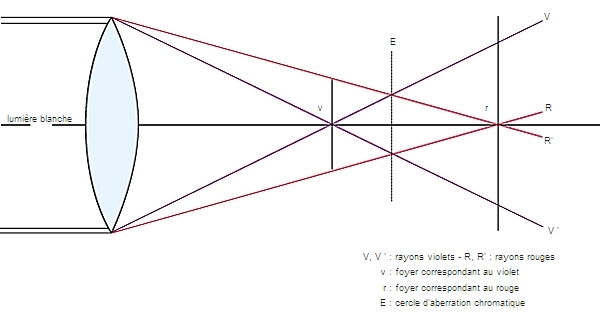
Si la lumière blanche émise par un point lumineux objet est réfractée différemment selon les radiations, l'image a une certaine largeur, et ses bords sont irisés. Cela est dû à la variation de l'indice de réfraction de la lentille avec la longueur d'onde de la lumière λ. En conséquence, les couples (A, A'ν) ne sont pas identiques ; il y a autant de A'ν que de radiations émises par le point lumineux objet A. Le milieu étant plus réfringent pour les courtes longueurs d'onde, le point A'bleu se trouve avant le point A'rouge le long de l'axe pour un point objet de l'axe. Il ne peut exister de stigmatisme global. Le problème est le même pour les points n'appartenant pas à l'axe. Il s'agit ici de l'aberration chromatique.
Pour y remédier, on associe plusieurs lentilles d'indices et de pouvoir dispersif différents. Cette découverte technique, réalisée en 1757 par un opticien londonien, John Dollond, infirmait la théorie de Newton : il pensait qu'il serait à jamais impossible de « corriger ce défaut inhérent à la nature même du verre ».
Les aberrations géométriques
L'aberration de sphéricité
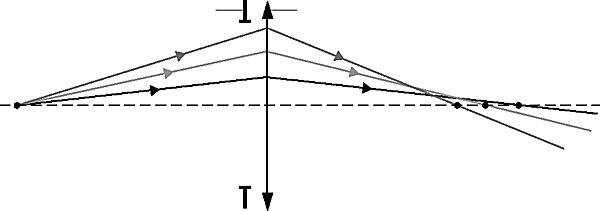
Considérons une lumière monochromatique. Si nous sortons des conditions de Gauss, à grande ouverture, les rayons formant l'image A' d'un objet A éloigné de la lentille ne convergent pas en un point car les rayons qui traversent la lentille sur sa périphérie sont beaucoup plus déviés que les rayons paraxiaux (rayons proches de l'axe) : par rapport à la partie centrale, les bords d'une lentille convergente sont trop convergents et les bords d'une lentille divergente sont trop divergents ; ce défaut, nommé aberration de sphéricité, est une aberration du premier ordre.
La coma
C'est une aberration de deuxième ordre. Une lentille ne donne pas une image ponctuelle d'un point situé dans le voisinage de l'axe principal si le faisceau issu de ce point est trop large. On obtient une tache floue dont la forme rappelle une comète, d'où le nom de coma donné à cette aberration.
L'astigmatisme
L'emploi de faisceaux étroits ne suffit pas pour obtenir les images exemptes de défauts. En effet, avec un pinceau lumineux très incliné sur l'axe principal de la lentille, à un point objet correspondent deux images distinctes. Cette aberration de troisième ordre se traduit par l'impossibilité d'obtenir simultanément une image nette d'un cercle et de ses rayons : lorsque le diamètre horizontal est net, le diamètre vertical est flou, et inversement.
La courbure de champ
C'est aussi une aberration de troisième ordre. Même si l'astigmatisme est corrigé, l'image d'un plan étendu, normal à l'axe principal, est une surface courbe. Ce défaut est appelé courbure de champ.
La distorsion
C'est une aberration de quatrième ordre. Elle ne compromet pas la netteté mais la fidélité de l'image : les points les plus périphériques sont trop proches ou trop éloignés de l'axe optique. La position de l'image est modifiée.
Le grandissement linéaire des images croît quand on s'écarte de l'axe de la lentille. Ainsi, à une ligne droite ne passant pas par l'axe correspond une ligne courbe dont la concavité est tournée vers le centre de l'image (distorsion en barillet) ou dans le sens opposé (distorsion en coussinet ou en croissant).
Un système exempt de distorsion est dit orthoscopique.
Les remèdes
Un instrument d'optique ne peut être seulement utilisé dans les conditions strictes de Gauss et le problème de l'atténuation des aberrations est très difficile, car les conditions requises pour leur correction sont souvent opposées. Suivant le but, l'opticien opère des associations de lentilles, pour lesquelles il joue sur les formes, les matières et les emplacements respectifs des diverses lentilles de façon que les défauts se compensent. On peut également chercher à disposer judicieusement des diaphragmes.
Les lentilles spéciales
Les lentilles cylindriques sont limitées par deux surfaces cylindriques dont les génératrices sont parallèles ou par une surface cylindrique et un plan. Les lentilles sphérocylindriques sont limitées par une sphère et un cylindre. Certaines lentilles sont limitées par deux surfaces toriques, l'une des faces pouvant être remplacée par un plan ou une sphère ; ces lentilles toriques servent principalement à la correction de l'astigmatisme des yeux. Les lentilles à échelons de Fresnel, utilisées dans les phares, permettent d'éliminer sommairement mais suffisamment l'aberration de sphéricité axiale. La diminution d'épaisseur de la partie centrale permet des réalisations de grande dimension. Le risque d'échauffement et de grosse perte d'énergie est ainsi diminué.