matrice d’une application linéaire (suite)

Transposée d’une matrice

La transposée d’une matrice A s’obtient en permutant ses lignes et ses colonnes. Si A a p lignes et n colonnes, sa transposée, notée ^tA, a n lignes et p colonnes ; si 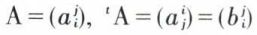et ceci
∀i ∈ {1, 2, ..., p} et ∀j ∈ {1, 2, ..., n},
les éléments si la matrice est carrée, ne changent pas de place. On a
^t(^tA) = A      ^t(A + B) = ^tA + ^tB      ^t(BA) = ^tA ^tB
et, par suite, ^t(A₁ A₂ ... A_n) = tA_n ^tA_n–1 ... ^tA₂ ^tA₁.

Matrice carrée

Une matrice est carrée lorsque le nombre de ses lignes est égal à celui de ses colonnes. Ce nombre est l’ordre de la matrice. Les matrices carrées d’ordre n, désignées souvent par M_nn (K) ou M_n (K) munies de l’addition et de la multiplication des matrices, forment un anneau non commutatif à l’élément unité.

En effet, pour deux matrices carrées d’ordre n, A et B, on peut définir les deux produits AB et BA, puisque le nombre de lignes est égal à celui des colonnes. Mais, en général, AB ≠ BA. D’où la non-commutativité de la multiplication des matrices. Mais la matrice-unité

qui n’a que des zéros partout, sauf sur la diagonale principale, où il n’y a que des 1, commute avec toute matrice de M_nn (K). Il est alors facile de vérifier la structure d’anneau non commutatif et unitaire.

Matrice carrée régulière

Une matrice carrée A est régulière ou inversible s’il existe une matrice A′ et une seule, du même ordre, telle que AA′ = A′A = I, I étant la matrice unité du même ordre que A et A′. En désignant par A^–1 la matrice A′, il résulte des deux égalités AA^–1 = A^–1 A = I que la matrice A^–1 est aussi régulière.

Pour qu’une matrice carrée A de M_nn (K) soit régulière, il faut et il suffit que ses n vecteurs-colonnes (ou lignes) soient linéairement indépendants. Cette condition est encore équivalente à la suivante : le déterminant de la matrice A est non nul ; on note
dét. A ≠ 0 ou |A| ≠ 0.

L’ensemble des matrices carrées inversibles d’ordre n, muni de la multiplication des matrices, est un groupe non commutatif, l’élément unité étant I = I_nn. L’inverse du produit des matrices A₁, A₂, ..., A_n est la matrice produit En utilisant l’associativité du produit, on voit que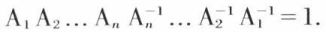

Déterminant d’une matrice carrée A = (a_ij)

C’est le déterminant des vecteurs-colonnes (ou lignes) de la matrice A (puisqu’un déterminant est invariant quand on effectue sur ces coefficients une symétrie par rapport à la diagonale principale) :
dét A = dét (a_ij) = |a_ij|.
Le déterminant du produit de deux matrices est égal au produit des déterminants de ces matrices :
si C = BA, dét C = dét B ⋅ dét A.

Si le produit de deux matrices n’est pas commutatif, le produit de deux déterminants est commutatif ; ainsi,
dét AB = dét BA = dét A ⋅ dét B
En effet, un déterminant n’est pas modifié par échange des lignes ou des colonnes. De plus, comme le corps K sur lequel sont construits les espaces E_n et F_n est commutatif (dans les applications K = ℝ ou K = ℂ), on a
dét A ⋅ dét B = dét B ⋅ dét A,
puisque ces deux déterminants sont des scalaires de K.

Matrices carrées particulières

• Une matrice symétrique est une matrice identique à sa transposée ; ainsi,

• Une matrice antisymétrique est une matrice identique à l’opposée de sa transposée : 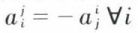et j ∈ {1, 2, ..., n} ; il en résulte, en particulier que donc que 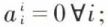une matrice antisymétrique n’a que des zéros sur sa diagonale principale. Comme tout déterminant symétrique gauche d’ordre impair est nul (antisymétrique), il en résulte que toute matrice antisymétrique d’ordre impair est singulière (non régulière).

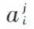• Une matrice diagonale est une matrice dans laquelle pour i ≠ j ; les éléments sont quelconques.

• Une matrice triangulaire est une matrice dans laquelle 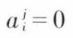pour j > i ou pour j < i, l’un excluant l’autre ; ainsi,

est une matrice triangulaire.

Toute matrice carrée peut être décomposée d’une façon et d’une seule en une somme de deux matrices dont lune est symétrique et l’autre antisymétrique. Cherchons, pour une matrice A donnée, les matrices B et C telles que A = B + C avec B = ^tB (symétrique) et C = – ^tC (antisymétrique). Du système A = B + C et ^tA = ^tB + ^tC = B – C, on tire

ce qui détermine B et C de façon unique et satisfaisant bien aux conditions imposées.

Changement de bases

L’espace E_n étant rapporté à la base et l’espace F_p à la base 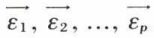, le vecteur 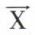de l’espace E_n est transformé en un vecteur 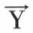de l’espace F_p par l’application u, de matrice A, tel que Y = AX = (a_ij) X. L’application u est indépendante des bases choisies pour les espaces E_n et F_p, sinon elle n’aurait plus de sens. Cette application a les mêmes effets sur les vecteurs de E_n quelle que soit la base, mais sa matrice A est remplacée par une matrice A′, que l’on doit chercher, quand on rapporte les espace E_n et F_p aux bases Si le changement de base dans l’espace E_n se traduit par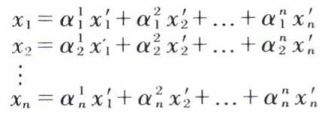

avec P = (a_ij), X et X′ étant les matrices-colonnes d’un même vecteur 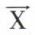de l’espace E_n,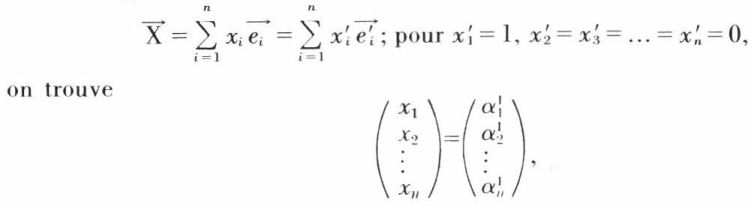

c’est-à-dire que le vecteur a pour composantes dans la base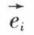

De même, on trouve que a pour composante dans la base 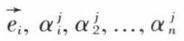ou 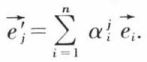On a donc E′ = ^tPE, E et E′ désignant les matrices unicolonnes des bases 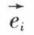et pour i = 1, 2, ..., n. Il est important de noter comment lune des deux relations X = PX′ ou E′ = ^tPE permet la connaissance de l’autre. En général, on connaît E′ = ^tPE. Il faut aussi remarquer que la matrice P est nécessairement régulière, puisque sa transformée ^tP a en vecteurs-colonnes les composantes des n vecteurs 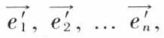qui sont linéairement indépendants : elle a donc ainsi un déterminant non nul.