matrice d’une application linéaire (suite)
Si Q définit le changement de base dans l’espace Fp, c’est-à-dire si Y = QY′, Q a en vecteurs-colonnes les composantes des vecteurs 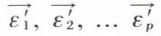 dans la base
dans la base 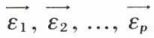 , et Q est régulière ; par suite, Y′ = Q–1Y, Q–1 étant l’inverse de Q. Comme Y = AX et que X = PX′, on a donc
, et Q est régulière ; par suite, Y′ = Q–1Y, Q–1 étant l’inverse de Q. Comme Y = AX et que X = PX′, on a donc
Y′ = Q–1 APX′ ou A′ = Q–1 AP.
Dans cette relation, A est une matrice à p lignes et n colonnes, Q–1 une matrice carrée d’ordre p, P une matrice carrée d’ordre n, A′ une matrice à p lignes et n colonnes. Les matrices A et A′ sont dites équivalentes.
• Matrices équivalentes. Deux matrices A et A′ à p lignes et n colonnes sont dites équivalentes s’il existe deux matrices régulières R et T d’ordres respectifs p et n telles que A′ = RAT ; la relation ainsi définie est une relation d’équivalence.
• Matrices semblables. On considère souvent le cas d’endomorphismes, c’est-à-dire qu’alors En = Fp et p = n. Par suite, Q = P et
Y′ = P–1 APX′ ou A′ = P–1 AP.
Deux matrices A et A′ sont dites semblables si elles sont du même ordre, n, et s’il existe une matrice carrée P régulière d’ordre n telle que A′ = P–1 AP.
Si A′ = P–1 AP et B′ = P–1 BP,
A′ + B′ est semblable à A + B ;
λ A est semblable à λ A′, λ ∈ K, corps de base ;
A′B′ est semblable à AB ;
A′n est semblable à An ;
si A est régulière, de même A′ ;
tA est semblable à tA′.
Valeurs propres, vecteurs propres, diagonalisation d’une matrice carrée
f étant un endomorphisme d’un espace En sur un corps commutatif K, 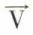 est un vecteur propre de f pour la valeur propre λ si
est un vecteur propre de f pour la valeur propre λ si 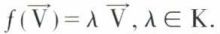
La recherche des vecteurs propres se ramène donc d’abord à celle des valeurs propres ; λ est une valeur propre s’il lui correspond au moins un vecteur propre. L’ensemble des vecteurs propres correspondant à une valeur propre forme un sous-espace vectoriel de En. Un sous-espace propre est un sous-espace des vecteurs propres associés à une valeur propre donnée.
Recherche des valeurs et vecteurs propres
L’endomorphisme f ayant pour matrice 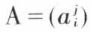 pour i et j = 1, 2, ..., n, un vecteur
pour i et j = 1, 2, ..., n, un vecteur 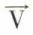 de matrice-colonne
de matrice-colonne 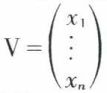 est propre pour la valeur propre λ de K, si et seulement si AV = λ IV, ou (A – λ I) V = 0, I étant la matrice unité d’ordre n, ce qui donne le système
est propre pour la valeur propre λ de K, si et seulement si AV = λ IV, ou (A – λ I) V = 0, I étant la matrice unité d’ordre n, ce qui donne le système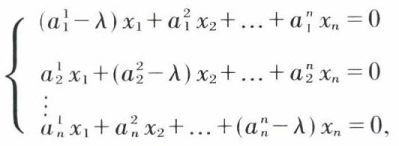
qui est homogène et qui n’admet de solutions différentes de la solution banale 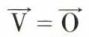 que si son déterminant est nul. Ainsi, les valeurs propres sont données par l’équation dét (A – λ I) = 0 ou
que si son déterminant est nul. Ainsi, les valeurs propres sont données par l’équation dét (A – λ I) = 0 ou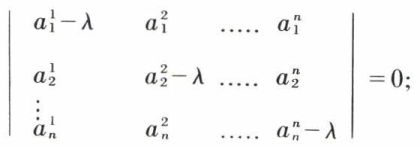
dét (A – λ I) = 0 est l’équation caractéristique de la matrice A ; si dans le système (I), on remplace λ par une racine λi (i = 1, 2, ..., n) de l’équation caractéristique, le rang de ce système est strictement inférieur à n. Lorsque ce rang r est égal à n – 1, par exemple, ce qui est le cas si λi est racine simple de l’équation caractéristique, les n composantes x1, x2, ..., xn sont fournies par un système de n – 1 équations à n inconnues ; ces composantes sont donc connues à un facteur multiplicatif près, et le sous-espace propre relatif à λi est de dimension 1 (droite vectorielle). Si, pour λ = λi, r < n – 1, ce qui est le cas pour une valeur propre λi d’ordre 2 au moins, il se peut que l’on puisse calculer les composantes x1, x2, ..., xn d’un ou de plusieurs vecteurs propres.
• Propriétés de l’équation caractéristique.
1. Elle est invariante dans un changement de base. En effet, si le changement de base est défini par
X = PX′, Y′ = P–1 APX′ ou A′ = P–1 AP,
les deux matrices A et A′ représentent le même endomorphisme f de En, mais dans deux bases différentes. L’équation caractéristique de A′ est
dét (A′ – λ I) = dét (P–1 AP – λ I) =
= dét (P–1 AP – P–1 λ IP) = 0 =
= dét [P–1(A – λ I)P] =
= dét P –1 ⋅ dét (A – λ I) ⋅ dét P = dét (A – λ I),
puisque dét P ⋅ dét P–1 = 1, car PP–1 = 1.
2. Les valeurs propres sont donc indépendantes de la base ; il en est de même des vecteurs propres, mais ceux-ci ont des composantes différentes dans deux bases différentes.
3. L’équation caractéristique est de degré n, puisque le déterminant du système (I) est d’ordre n ; il y a donc n valeurs propres, distinctes ou confondues.
4. Si l’on développe dét (A – λ I) suivant les éléments d’une ligne ou d’une colonne, on constate que l’équation caractéristique se met sous la forme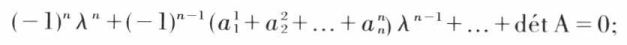
par suite, la somme des racines, c’est-à-dire des valeurs propres, est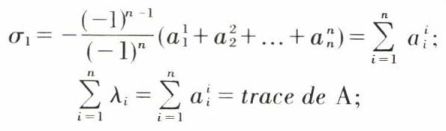
de plus, le produit des racines est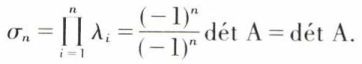
Le produit des valeurs propres est égal au déterminant de A. Par suite, si A est singulière, dét A = 0, l’une, au moins, des valeurs propres est nulle.
Diagonalisation d’une matrice carrée
À toute racine d’ordre p de l’équation caractéristique correspond un sous-espace propre de dimension au plus égale à p. Si à chaque racine correspond un sous-espace dont la dimension est égale à l’ordre de cette racine, on peut trouver pour chaque racine un nombre de vecteurs propres égal à l’ordre de cette racine ou à la dimension du sous-espace correspondant. On peut donc trouver au total n vecteurs propres ; ces n vecteurs propres forment une base de l’espace En. Si P est la matrice ayant en vecteurs-colonnes ces n vecteurs et si l’on prend ces vecteurs propres comme nouvelle base, les formules de changement de base sont
X = PX′ et Y = PY′ avec A′ = P–1 AP et Y′ = A′X′.
La matrice A′ transforme un vecteur propre 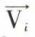 correspondant à la valeur propre λi en un vecteur λi
correspondant à la valeur propre λi en un vecteur λi 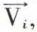 et, comme la base choisie est celle des vecteurs propres
et, comme la base choisie est celle des vecteurs propres 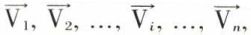 la i-ème colonne de A′, qui est formée des composantes de λi
la i-ème colonne de A′, qui est formée des composantes de λi 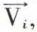 transformée de
transformée de 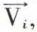 est
est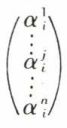
avec 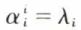 et
et 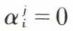 pour i ≠ j, cela étant valable pour tout i = 1, 2, ..., n. La matrice A′ est donc diagonale et égale à
pour i ≠ j, cela étant valable pour tout i = 1, 2, ..., n. La matrice A′ est donc diagonale et égale à
plusieurs des éléments λi pouvant être égaux. On peut donc trouver dans ce cas une matrice diagonale A′ = P–1 AP semblable à la matrice A. Ce cas se produit en particulier lorsque toutes les racines de l’équation caractéristique sont simples, c’est-à-dire toutes distinctes.
• Applications de la diagonalisation.




