aléatoire (variable) (suite)

Loi de probabilité d’une variable aléatoire

Pour toute variable aléatoire X, définie sur un univers Ω, il est possible de définir une probabilité P′ sur l’univers-image Ω′ en associant à toute valeur numérique x de Ω′ la probabilité de l’événement composé de toutes les éventualités dont l’image par X est x. La nouvelle probabilité P′ ainsi obtenue est la loi de probabilité de la variable aléatoire X. On en a un exemple par le tableau ci-dessus.
1. Variable aléatoire discrète. C’est une variable dont l’univers-image est fini ou infini dénombrable. Les deux exemples précédents concernent des variables discrètes.
2. Variable aléatoire continue. C’est une variable susceptible de prendre toute valeur d’un intervalle [a, b], éventuellement infini.
Exemple : On choisit au hasard un point sur l’intervalle [0, 1]. L’abscisse de ce point, X, est susceptible de prendre toute valeur comprise entre 0 et 1, et cela avec une probabilité nulle. En effet, si la probabilité d’une telle valeur n’était pas nulle, elle serait constante, par symétrie, et le segment [0, 1] ne pourrait avoir 1 comme probabilité. Par contre, la probabilité attachée à un intervalle (a, b) où est proportionnelle à la longueur de cet intervalle ; elle vaut k(b – a) et k = 1 pour que la probabilité du segment [0, 1] soit égale à 1. Ainsi
Pr {a < X < b} = b – a.
La variable aléatoire ainsi définie est appelée variable uniforme sur [0, 1] et notée .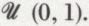

Fonction de répartition d’une variable aléatoire

C’est la fonction F définie pour tout x réel par la relation
F(x) = Pr {X < x}.
1. Variable discrète. La variable aléatoire X est susceptible de prendre les valeurs x_i avec les probabilités p_i, pour i = 1, 2, ..., n, ou pour i = 1, 2, ..., n, ...

et, si a et b sont deux nombres réels quelconques.

Exemple : Dans l’exemple simple du jeu de dés à un dé, on a la loi de probabilité définie par le tableau suivant :

Ce qui donne la fonction de répartition suivante :

On vérifie sur cet exemple des propriétés valables dans le cas général.
Pour x petit
Pour x grand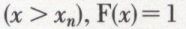
Si X peut prendre une infinité de valeurs (i = 1, 2, ..., n, ...), F(x) → 1 quand x → + ∞.
Enfin, la fonction F est croissante au sens large.
2. Variable continue. Une variable aléatoire continue X est définie par sa fonction de répartition F, qui donne, comme pour une variable discrète, la probabilité pour que X soit inférieure à x :
F(x) = Pr{X < x}
La fonction F est continue, positive, monotone non décroissante, nulle pour x = – ∞, égale à 1 pour x = + ∞.
Exemple : La fonction de répartition F de la variable uniforme est définie par

Densité de probabilité. Pour une variable continue, la probabilité attachée au segment [a, b] est

La densité moyenne de probabilité entre a et b est le rapport

La densité moyenne sur l’intervalle [x, x + dx] est alors

et la limite de cette quantité, quand dx tend vers zéro, est la densité de probabilité en x, et l’on a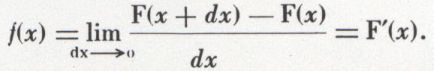

La densité de probabilité en un point est la dérivée de la fonction de répartition en ce point. Comme F est non décroissante, f est non négative et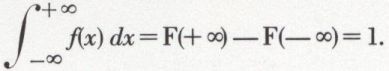

Caractéristiques d’une loi de probabilité

Espérance mathématique

a) Variable discrète. L’espérance mathématique d’une variable discrète X prenant les valeurs x_i avec les probabilités p_i, pour i = 1, 2, ..., n est la quantité

Si les valeurs que peut prendre X sont en infinité dénombrable, il se peut que la série ne soit pas convergente. On dit dans ce cas que l’espérance n’existe pas. Si, au contraire, la série converge, la somme de cette série est l’espérance de X.
Exemples.
1. Si X est le point amené par un dé à six faces, l’espérance mathématique est

2. Si X est le nombre de lancers nécessaires pour amener pile au jeu de pile ou face.

Le calcul de la somme de cette série se fait à l’aide de la formule du binôme généralisée, valable pour |x| < 1

Pour on obtient

b) Variable continue. L’espérance mathématique de la variable aléatoire continue susceptible de prendre toute valeur comprise entre a et b est l’intégrale

quand elle existe, f étant la densité de probabilité.
Exemple.
Pour la variable uniforme , F(x) = x, f(x) = 1 et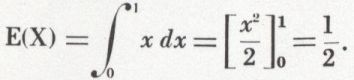

Les bornes a et b peuvent être infinies.

c) Propriétés de l’espérance mathématique. À partir d’une variable aléatoire X définie sur un univers Ω, on peut définir les variables aléatoires X + h et hX, h étant une constante quelconque. On obtient les valeurs possibles de ces variables en ajoutant h aux valeurs que peut prendre X ou en les multipliant par h, les probabilités correspondantes étant les mêmes. On démontre alors que E (X + h) = E (X) + h ; E (hX) = h E(X). La première égalité entraîne que
E [X – E (X)] = 0,
pour h = E (X) : la variable centrée X – E (X) a une espérance nulle. Si X et Y sont deux variables aléatoires définies sur un même univers, E (X + Y) = E (X) + E (Y).
On résume les relations indiquées par une seule :
E (αX + βY) = αE (X) + βE (Y),
qui traduit le caractère linéaire de l’espérance mathématique. Mais, en général, on n’a pas
E (XY) = E (X) E (Y).
L’égalité n’est valable que si les deux variables X et Y sont indépendantes. Si, par exemple, X prend les valeurs x_i avec les probabilités p_i, pour i = 1, 2, ..., n, et si Y prend les valeurs y_j avec les probabilités g_j, pour j = 1, 2, ..., m, les variables X et Y sont indépendantes si les événements X = x_i et Y = y_i le sont, c’est-à-dire si
Pr {X = x_i et Y = y_j} = Pr {X = x_i} × Pr {Y = y_j} = p_iq_j.
Il suffit, pour montrer que l’égalité E(XY) = E(X) E(Y) n’a pas toujours lieu, de considérer deux variables X et Y égales et prenant les valeurs 0 et 1 avec les probabilités , comme au jeu de pile ou face, où les deux variables valent 0 si face sort et 1 si pile sort. On voit que

Mais Z = XY prend aussi les valeurs 0 ou 1, respectivement si face ou pile sort et

Les propriétés de l’espérance mathématique énoncées ci-dessus permettent de calculer l’espérance de certaines variables aléatoires fonctions d’autres variables aléatoires.