La relation « a un cardinal inférieur ou égal à » est réflexive, transitive et antisymétrique ; c’est une relation d’ordre. Si on admet l’axiome de Zermelo, ou axiome du choix, l’ordre ainsi obtenu est total, c’est-à-dire que la classe des nombres cardinaux est totalement ordonnée par la relation considérée. Cet ordre présente en outre la propriété suivante : toute sous-classe de nombres cardinaux possède un plus petit élément, ce que l’on résume en disant que la classe des nombres cardinaux est bien ordonnée. En particulier, la classe des nombres cardinaux elle-même possède un plus petit élément, ou 1^er élément, puis un 2^e élément, un 3^e, ..., un n^-ième élément, n étant un entier quelconque. Ces éléments constituent la classe des nombres cardinaux finis. Il y a également la classe des nombres cardinaux infinis. Cette classe n’est pas vide puisqu’elle contient au moins le cardinal de l’ensemble ℕ des entiers naturels, qui est infini. Mais il n’est pas évident qu’il existe des ensembles infinis dont le cardinal soit supérieur à celui de l’ensemble ℕ ; il n’est pas évident non plus que les ensembles infinis n’ont pas tous la même puissance. Cependant, quel que soit l’ensemble E, l’ensemble des parties de E a une puissance strictement supérieure à celle de E. Ainsi a une puissance supérieure à celle de ℕ, puis a une puissance supérieure à celle de ℕ′, etc.

La classe des cardinaux des ensembles infinis possède, elle aussi, un plus petit élément, que l’on note 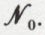Ce cardinal est égal à | ℕ |, car, comme ℕ est infini, on a sûrement d’autre part, de tout sous-ensemble infini A, on peut extraire une suite infinie a₀, a₁, ..., a_n, ... d’éléments distincts, ce qui entraîne cela est vrai en particulier pour d’où

Puissance du dénombrable

C’est la puissance de tout ensemble dont le cardinal est égal à c’est-à-dire de tout ensemble dont les éléments peuvent être rangés en une suite infinie x₁, x₂, ..., x_n,... indexée par les entiers naturels 1, 2, ..., n,...

Puissance du continu

L’ensemble des parties de ℕ a une puissance strictement supérieure à celle de ℕ : c’est la puissance du continu ; c’est aussi la puissance de l’ensemble des nombres réels du segment [0, 1] et de l’ensemble des nombres réels ℝ tout entier.

1. L’ensemble a même puissance que les nombres de [0, 1].

En effet, toute partie de ℕ peut être représentée par une suite illimitée de 0 et de 1 ; par exemple, la suite u = (0,0,1,1,0,1,0,1,1,0,...), que l’on compare à ℕ = {1,2,3,...}, représente la partie A = {3,4,6,8,9} de ℕ, car les chiffres 0 et 1 de u indiquent respectivement la non-appartenance et l’appartenance à A des nombres de ℕ de même rang

Mais toute suite de 0 et de 1 représente le développement binaire ou dyadique d’un nombre compris entre 0 et 1, et, pour tout nombre α tel que 0 < α < 1, il existe une suite u = (a₁,a₂,...,a_n,...) avec a_n = 0 ou a_n = 1 et α = 0, a₁a₂...a_n..., α étant écrit dans le système binaire. Par exemple, pour α = 0,10 110..., écrit dans le système binaire, u = (1,0,1,1,0,...) ; α est le nombre dans le système décimal. Cependant, la représentation dyadique d’un nombre du segment [0, 1] n’est pas toujours unique. Dans certains cas, il peut y avoir deux représentations pour un même nombre. Par exemple, pour α = 0,001 0... dans le système binaire ( dans le système décimal), le nombre 0,0001... du système binaire vaut et est égal à α ; d’où les deux représentations pour α : 0,001 0... et 0,000 1... Ce cas est celui de tous les nombres de la forme Mais l’ensemble de ces nombres est dénombrable. Il en résulte que l’ensemble des nombres de [0, 1] a même puissance que l’ensemble des représentations dyadiques correspondantes, c’est-à-dire même puissance que .

2. L’ensemble ℝ a même puissance que [0, 1]. Le segment [0, 1] a même puissance que l’intervalle ]0, 1[ ; celui-ci a même puissance que l’intervalle ]– 1, + 1[, car on passe de l’intervalle ]0, 1[ à l’intervalle ]– 1, + 1[ par la bijection enfin, on passe de l’intervalle ]– 1, + 1[ à l’ensemble des nombres réels ℝ par la bijection ainsi, l’ensemble des nombres réels ℝ a même puissance que le segment [0, 1]. L’ensemble ℝ des nombres réels a la puissance du continu, c’est-à-dire la puissance de , qui est strictement supérieure à celle du dénombrable ou puissance de ℕ. L’ensemble des points du plan euclidien a la puissance du continu.

E. S.

➙ Application / Ensemble / ℕ / ℝ.

 P. Dubreuil, Algèbre, cahiers scientifiques, fasc. XX (Gauthier-Villars, 1954). / L. Chambadal et J. L. Ovaert, Cours de mathématiques, t. I : Notions fondamentales d’algèbre et d’analyse (Gauthier-Villars, 1966).