calcul des prédicats (suite)

1. Les variables liées ont longtemps été appelées des variables apparentes. En effet, l’écriture ci-dessus, quoique plus commode, apporte exactement la même information que la suivante :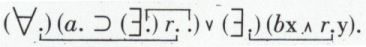

Il découle de là que le nom d’une variable liée (variable apparente) est inessentiel et que l’on peut indifféremment écrire

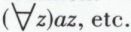
2. Il est maintenant possible de préciser la définition d’une forme propositionnelle et celle d’une proposition. Toute ebf qui contient au moins une variable d’objet libre est une forme propositionnelle, sinon c’est une proposition.

3. Il faut encore noter que seules les variables d’objet peuvent être liées. C’est la raison pour laquelle on parle de la logique des prédicats du premier ordre. Si l’on s’autorisait à lier aussi les variables de prédicat, si l’on pouvait écrire par exemple 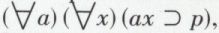on parlerait de la logique des prédicats du deuxième ordre.

On aura remarqué que la définition des ebf permet de faire figurer une variable de proposition dans le champ d’un quantificateur. Cela ne lie évidemment pas la variable de proposition, puisque les quantificateurs utilisés ici sont toujours au nom d’une variable d’objet. Il revient ainsi au même d’écrire p ou 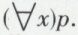Toutefois, dans certains cas, l’insertion d’une variable de proposition dans le champ d’un quantificateur peut être significative.

Considérons, pour voir la chose, les deux expressions suivantes :
Supposons que l’univers du discours soit réduit à l’ensemble Ω = df {x₁, x₂}. Dans ces conditions, les expressions (a) et (b) deviennent (a′) (ax₁ ⋀ ax₂) ⊃ p
et (b′) (ax₁ ⊃ p) ⋀ (ax₂ ⊃ p).
Ici, ax₁, ax₂ et p sont trois propositions, et il est possible de calculer les tables de vérité de (a′) et de (b′) [v. calcul des propositions] :

On voit que (b′) implique (a′) sans lui être équivalente.

Règles et schémas d’axiomes

Plaçons-nous d’abord dans la perspective de la déduction naturelle. Le calcul des propositions fournit déjà les règles propres à introduire et à éliminer les opérateurs propositionnels. Il ne reste donc qu’à fournir des règles pour les quantificateurs.

Introduction de ∀

Le problème peut s’énoncer de la façon suivante : si Ω est un ensemble d’objets et a un prédicat, trouver les conditions auxquelles doit satisfaire une déduction pour qu’il soit légitime de conclure

Dans le cas où Ω est un ensemble fini, le problème est théoriquement simple. Il suffit de démontrer successivement ax₁, ax₂, ... ax_n. En réitérant l’usage de la règle ⋀i (v. calcul des propositions), on obtient ax₁ ⋀ ax₂ ⋀ ... ⋀ ax_n, qui n’est rien d’autre que 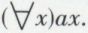Mais, pour certains ensembles finis, une telle procédure peut déjà être pratiquement irréalisable. Elle l’est toujours pour les ensembles infinis. La solution consiste alors à démontrer ax pour x quelconque. L’idée du quelconque n’est pas très facile à définir. Il suffit heureusement ici de retenir un seul de ses aspects : un x quelconque doit être un représentant des éléments de Ω, dont on ne retient aucune autre propriété. Cela implique deux conditions :
(1) Faire la déduction qui conduira à ax sans formuler d’hypothèse ;
(2) Ne réitérer dans cette déduction aucune expression qui contiendrait la variable x libre. Une expression qui contient x libre, par exemple bx ⋁ cx, signifie que x jouit de la propriété b ou de la propriété c. En conséquence, le x en question n’est plus quelconque.

D’une façon générale, on obtient le schéma suivant :

La première barre verticale indique que l’on se trouve au cours d’une déduction. La seconde barre verticale, qui ne porte pas le petit trait horizontal de l’hypothèse et qui est précédée de X, indique que l’on ne suppose rien sur X et qu’il est interdit d’y réitérer une expression qui contient cette variable X libre. Enfin, la justification de la ligne n + 1 se fait au nom de toute la sous-déduction 1 à n, dite sous-déduction stricte.

Élimination de ∀

La règle repose simplement sur le fait que, si une propriété est valable pour tous les éléments d’un ensemble Ω, elle est vraie pour un élément quelconque.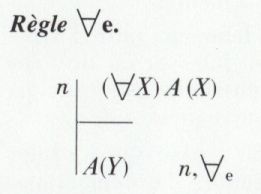

Le passage de A(X) à A(Y) signifie qu’on a le droit de substituer une variable Y à la variable X.

Il faut toutefois prendre deux précautions.
(1) L’opération de substitution exige que, s’il y a changement de variable, le changement soit effectué à chaque mention de la variable. Soit ainsi l’expression ax ⋀ bx. Les expressions suivantes résultent d’une substitution, la dernière étant un cas limite : ay ⋀ by, az ⋀ bz, ax ⋀ bx. En revanche, ax ⋀ bx, ay ⋀ by ne résultent pas de substitutions.
(2) Considérons l’expression 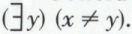Intuitivement définie sur les nombres naturels, elle est vraie : pour tout nombre x, il en existe un y qui est différent de x. La règle permet alors d’écrire par exemple 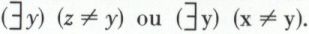Mais on voit immédiatement que l’on ne saurait substituer y à x sans aboutir à une contradiction : 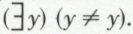Cela tient au fait que le premier y devrait être libre, mais que nos conventions d’écriture le lient. Il faut donc éviter de telles confusions, et nous dirons que seule une variable Y qui est libre pour X peut être substituée à X dans cette règle.

Remarque. Il est évident que X est toujours libre pour X.

Introduction de ∃

Si y est le nom d’un élément de Ω et si l’on a pu démontrer par exemple ay, c’est-à-dire que y jouissait de la propriété a, on peut alors affirmer qu’il existe au moins un élément de Ω qui possède la propriété a, donc que 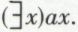Nous poserons donc d’une façon générale la règle suivante :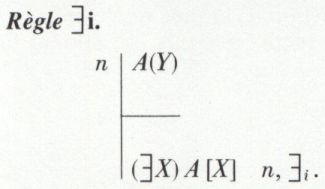

Il faut, bien entendu, que X soit libre pour Y. D’autre part, le passage de A(Y) à A[X], avec des crochets carrés, veut indiquer que l’on peut remplacer Y par X. Contrairement à la substitution, le remplacement n’exige pas, si l’on fait un changement, de le faire à chaque mention.