calcul des prédicats (suite)

Supposons ainsi que l’on ait l’expression ax ⋁ bx et que l’on apprenne ensuite que x est x₁. Il est clair que l’on peut remplacer x par x₁, c’est-à-dire que les expressions ax₁ ⋁ bx, ax ⋁ bx₁, ax₁ ⋁ bx₁ sont toutes trois correctes.

Élimination de ∃

Pour expliquer les conditions assez spéciales de la règle, nous allons utiliser un exemple naïf.

Supposons que l’on sache que, dans Ω, «  a menti ».

On peut évidemment faire l’hypothèse que x est Jules et en tirer les conséquences possibles, par exemple que « Jules manque de loyauté ».

Mais on voit aussi que « Jules manque de loyauté » ne dépend pas seulement de ce que a menti », mais encore du choix particulier et arbitraire de Jules comme menteur.

En revanche, si l’on parvient à une proposition comme « le contrat a été rompu », proposition qui ne mentionne plus Jules, alors peu importe que le raisonnement se soit fait sur Jules ou sur quelqu’un d’autre. Le fait que le contrat a été rompu ne dépend plus que de la prémisse existentielle.

Ce n’est d’ailleurs pas tout.

Supposons que, en cours de déduction, l’on ait fait appel à une autre proposition qui mentionnait le nom de Jules. Cela aurait conduit à faire dépendre la conclusion d’autre chose encore que de la seule connaissance qu’il existait un menteur.

Ce sont ces exigences qu’exprime la règle suivante :

À la ligne n, on fait une hypothèse sur l’élément qui est A (Jules dans l’exemple). Le P de la ligne m doit signifier que cette expression ne contient pas X libre. Le retour en arrière du P à la ligne l marque que l’on s’est rendu indépendant de la sous-déduction n à m. Enfin, le X en exergue à la ligne n rappelle qu’il est interdit de réitérer des expressions qui contiendraient X libre.

Ces règles, jointes à celles du calcul des propositions, permettent d’établir les deux schémas de théorèmes suivants :

Il s’ensuit que les deux quantificateurs ne sont pas indépendants l’un de l’autre et qu’il est possible de définir, par exemple, à partir de

Cela va nous permettre de fournir une présentation axiomatique économique du calcul des prédicats.

Nous allons nous donner tout d’abord des schémas d’axiomes qui équivalent à ceux du calcul des propositions. La seule différence sera que les métavariables prendront pour valeur les ebf du calcul des prédicats, c’est-à-dire qu’elles pourront désigner non seulement des propositions, mais encore des formes propositionnelles. À la place de P, Q, M (v. calcul des propositions), nous utiliserons les lettres A, B, C avec les conventions suivantes :
(1) Nous écrirons A, B, C dans les cas où il n’importe pas de savoir si ces expressions contiennent des variables libres ou non ;
(2) Nous écrirons A(X), B(X), etc., pour souligner le fait que l’expression contient la variable X libre ;
(3) Si une expression ne peut pas contenir une certaine variable libre, nous le dirons explicitement.

Posons alors les schémas suivants :

à condition que A ne contienne pas X libre. si, dans A, X n’est pas dans le champ d’un quantificateur au nom de Y.

Comme on le voit, A₁ à A₃ recouvrent le calcul des propositions. A₄ correspond à la règle et la restriction sur la présence de X libre résulte des remarques sur l’idée du quelconque. Enfin, A₅ correspond à la règle

Quant aux règles de transformation, dites aussi règles d’inférence (v. langages formels), elles sont les suivantes :
R₁ À partir de A et de A ⊃ B, on peut inférer B ;
R₂ À partir de A,on peut inférer

La règle R₁ est celle du modus ponens, et la règle R₂ est celle de la généralisation.

Remarques.

1. Les règles paraissent s’appliquer à n’importe quelles ebf de la forme donnée. En fait, puisque toute démonstration commence nécessairement par un axiome et qu’un axiome est un théorème, elles ne peuvent être utilisées que sur des théorèmes. Cette remarque est particulièrement importante pour la règle R₂, qui donne l’impression que, quelle que soit l’ebf A, il est possible de la généraliser. Mais, si l’on peut en effet passer, par exemple, de à 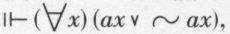on ne saurait passer de ax, qui n’est pas un théorème, à

2. Comme nous l’avons déjà noté à propos des ebf, le système permet d’écrire par exemple en appliquant R₂ à Mais cela est sans inconvénient.

L’étude des théorèmes du calcul montre plusieurs faits intéressants.

• 1. Dualité.

Elle existe entre ⋀ et ⋁ et entre sous la forme suivante :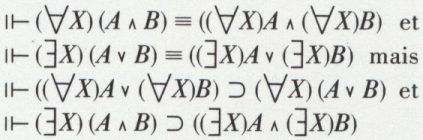

sans que les réciproques de ces derniers schémas de théorèmes ne soient valides.

• 2. Relations entre quantificateurs. On a :

sans, naturellement, que les réciproques ne soient valides.

• 3. Permutation des quantificateurs. On a les lois suivantes :

mais sans la réciproque.