calcul des prédicats (suite)

Remarques

1. Considérons le prédicat a′ = df être un homme illustre. Les deux propositions a′x₁ et a′x₂ sont vraies, de sorte que, dans cette perspective, a′ ne se distingue pas de a, pas plus que ne s’en distingueraient les prédicats « avoir écrit de nombreux ouvrages », « figurer au programme du baccalauréat », etc. Dans le présent système — et d’ailleurs dans tous ceux qui sont actuellement élaborés —, les prédicats ne sont considérés qu’en tant que, appliqués à des objets, ils produisent des propositions vraies ou fausses. Leur signification, au sens usuel du terme, n’est pas directement prise en considération. On exprime cela en disant que la logique des prédicats adopte un point de vue extensionnel.

2. Si Ω comporte n éléments, on pourra définir 2ⁿ prédicats distincts à une place. Tout cela se généralise aux prédicats à plus d’une place.

Tous et quelques

Une proposition est une expression dont il y a un sens à dire qu’elle est vraie ou qu’elle est fausse (v. calcul des propositions). Prenons pour Ω l’ensemble des nombres naturels et considérons le prédicat a = df être premier. L’expression ax, soit « x est (un nombre) premier », n’est pas une proposition au sens ci-dessus : elle n’est pas vraie, elle n’est pas fausse, elle est indéterminée. Nous dirons que c’est une forme propositionnelle.

Il existe divers procédés qui transforment une forme propositionnelle en une proposition. En voici trois :
(1) Donner à x une valeur déterminée de Ω, par exemple 13. On obtient bien alors la proposition « 13 est (un nombre) premier », qui est vraie ;
(2) Affirmer que le prédicat a s’applique à tous les éléments de Ω : « tous les x sont a ». On a bien une proposition. Elle est fausse avec l’interprétation donnée ici à a, mais cela ne lui enlève pas son statut de proposition ;
(3) Affirmer que le prédicat s’applique à l’un au moins des éléments de Ω : « il y a au moins un x qui est a », ce qui est une proposition vraie.

Introduisons alors les notations suivantes :
« tous les x sont a » ou « pour tout x, x est a » ou « pour tout x, ax » ;
« il y a (au moins) un x qui est a » ou « il y a un x tel que x est a » ou « il y a un x tel que ax ».

Les signes et sont appelés des quantificateurs. Le premier est le quantificateur universel, le second est le quantificateur existentiel.

Remarque. On trouve dans la littérature les écritures suivantes :
ou (x) ou Πx ; ou (Ex) ou Σx.

Soit Ω l’ensemble des candidats à une élection et soit a = df être élu. L’expression exprime que tous les candidats sont élus. Supposons alors que tel ne soit pas le cas, donc que cette proposition soit fausse. Elle peut manifestement l’être de deux façons :
(1) Aucun candidat n’est élu ;
(2) Certains candidats sont élus et d’autres pas.

On voit alors facilement que l’on obtiendra soit la proposition (1), soit la proposition (2) en plaçant de deux façons différentes l’opérateur de négation  :

D’autre part, l’expression 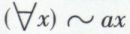est intuitivement équivalente à et l’expression Les axiomes et les règles qui suivent devront permettre d’établir ces équivalences sous forme de théorèmes.

L’appareil du calcul

Pour construire un calcul des prédicats, nous allons nous donner ce qui suit.

• (1) Trois classes de variables :
— des variables de proposition : p, q, m et éventuellement les mêmes lettres accentuées ;
— des variables d’objet : x, y, z, t, u, v et éventuellement les mêmes lettres accentuées ;
— des variables de prédicat :

etc., où n = 1, 2, 3, etc.

Remarques.

1. Les variables de proposition prennent leurs valeurs sur l’ensemble {1, 0}. (V. calcul des propositions.)

2. Les variables d’objet prennent leurs valeurs sur l’univers du discours, que nous ne spécifions pas.

3. Une variable de prédicat désigne un prédicat à n places. Il sera toutefois commode dans ce qui suit d’adopter les conventions suivantes :
a, b, c désigneront trois variables de prédicat à une place. Elles seront donc interprétées comme des propriétés ;
r, s désigneront deux variables de prédicat à deux places. Elles seront donc interprétées comme des relations binaires.

• (2) Deux classes d’opérateurs :
— les opérateurs propositionnels, parmi lesquels on aura (V. calcul des propositions.)
— les quantificateurs :

Dès lors, les expressions bien formées du système (les ebf) seront définies comme suit, étant entendu que les parenthèses sont ici utilisées de façon intuitive pour marquer l’ordre de construction des expressions.
(1) Une variable de proposition est une ebf.
(2) Si A est une variable de prédicat à n places et si X₁ ... X_n sont n variables d’objet, AX₁ ... X_n est une ebf.
(3) — (9) Si A et B sont des ebf et si X est une variable d’objet, 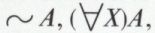(A ⋀ B), (A ⋁ B), (A ⊃ B), (A ≡ B), sont des ebf.

(10) Rien n’est une ebf, sinon par (1) — (9).

Ainsi, les formules suivantes sont des ebf :

Remarques.

Dans tout ce qui suit, nous économiserons autant que possible les parenthèses. Cela nous amènera à écrire par exemple p ⊃ ax au lieu de (p ⊃ ax) lorsque aucune ambiguïté n’en résultera.

Considérons maintenant les deux ebf suivantes :

Les crochets qui figurent dans (a) indiquent que les quantificateurs portent sur toute l’expression (ax ⋀ by) ⊃ rxy. Les crochets et les parenthèses servent donc ici à déterminer la portée ou le champ des quantificateurs, c’est-à-dire à marquer leur domaine d’action.

D’une façon générale, une variable d’objet qui se trouve dans le champ d’un quantificateur à son nom est dite liée. Une variable qui n’est pas liée est dite libre. Dans l’exemple suivant, les variables d’objet liées sont en italique et les variables d’objet libres en romain :

Remarques.