statique (suite)
Réduction des forces appliquées à un solide
On a intérêt à réduire, par des opérations élémentaires, les forces appliquées à un solide à un système aussi simple que possible. Les deux opérations les plus faciles et les plus fréquentes concernent le cas où les forces sont concourantes et le cas où elles sont parallèles.
• Forces concourantes
On peut les réduire à une force unique  ; le moment linéaire
; le moment linéaire  par rapport à un point O quelconque est la somme des moments des composantes. Si la force
par rapport à un point O quelconque est la somme des moments des composantes. Si la force  est nulle, les forces se font équilibre.
est nulle, les forces se font équilibre.
• Forces parallèles
• Cas de deux forces parallèles et de même sens. Les deux forces 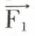 et
et  sont appliquées en deux points A1 et A2 d’un solide. En ces deux points, on applique deux forces
sont appliquées en deux points A1 et A2 d’un solide. En ces deux points, on applique deux forces 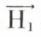 et
et  , égales et directement opposées, que l’on compose avec
, égales et directement opposées, que l’on compose avec 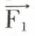 et
et  . On obtient deux forces
. On obtient deux forces 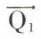 et
et  , qui concourent en un point M. Transportées en M, les deux forces
, qui concourent en un point M. Transportées en M, les deux forces 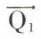 et
et  deviennent
deviennent 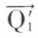 et
et 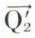 . On décompose
. On décompose 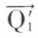 en deux forces
en deux forces  et
et 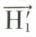 , égales et parallèles à
, égales et parallèles à 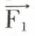 et
et 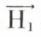 ; de même,
; de même, 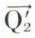 est décomposée en deux forces
est décomposée en deux forces  et
et  , égales et parallèles à
, égales et parallèles à  et
et  . Les forces
. Les forces 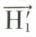 et
et  , égales et directement opposées, se détruisent ; les deux autres,
, égales et directement opposées, se détruisent ; les deux autres,  et
et  , dirigées dans le même sens, suivant la parallèle MA aux deux forces
, dirigées dans le même sens, suivant la parallèle MA aux deux forces 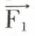 et
et  , se composent en une seule force
, se composent en une seule force  parallèle aux composantes et de même sens qu’elles. Pour déterminer la ligne d’action MA de la force
parallèle aux composantes et de même sens qu’elles. Pour déterminer la ligne d’action MA de la force  , il suffit de déterminer le point A, où elle coupe le segment de droite A1A2 ; ce point est entre A1 et A2.
, il suffit de déterminer le point A, où elle coupe le segment de droite A1A2 ; ce point est entre A1 et A2.
Les triangles F1Q1A1 et AA1M étant semblables, on a
De même, pour les triangles F2Q2A2 et AA2M, on a
En divisant membre à membre et du fait que H1 = H2, on a
Deux forces parallèles et de même sens ont une résultante parallèle de même sens, placée entre les composantes, égale à leur somme ; la ligne d’action de cette résultante divise la droite joignant les points d’application des composantes en deux segments inversement proportionnels aux composantes. Le point A ainsi obtenu est le point d’application de la résultante. Ce point reste le même si les composantes changent d’intensité, sans que leur rapport soit modifié.
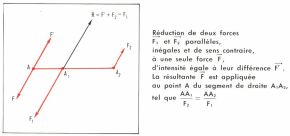
• Cas de deux forces parallèles, inégales et de sens contraires. Si 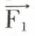 et
et  sont les deux forces appliquées en A1 et en A2
sont les deux forces appliquées en A1 et en A2  on prend, sur le prolongement de A2A1, du côté de la plus grande des forces
on prend, sur le prolongement de A2A1, du côté de la plus grande des forces 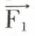 , un point A tel que
, un point A tel que  En ce point A, on applique deux forces égales et opposées
En ce point A, on applique deux forces égales et opposées  et
et 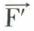 , d’intensité (F1 – F2), parallèles à
, d’intensité (F1 – F2), parallèles à 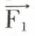 et à
et à  , l’une,
, l’une,  ayant le sens de
ayant le sens de 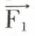 , l’autre,
, l’autre, 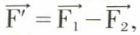 ayant le sens opposé. Les deux forces
ayant le sens opposé. Les deux forces 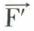 et
et  ont une résultante
ont une résultante  égale et opposée à
égale et opposée à  . Cette résultante de
. Cette résultante de  et de
et de 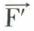 étant égale et opposée à
étant égale et opposée à 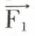 , l’ensemble
, l’ensemble  ,
, 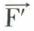 et
et 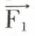 peut être supprimé, et il reste la force
peut être supprimé, et il reste la force  appliquée en A. Deux forces parallèles inégales et de sens contraires ont une résultante parallèle de même sens que la plus grande, placée à l’extérieur des composantes, égale à leur différence ; la ligne d’action de cette résultante divise la droite joignant les points d’application des composantes en deux segments inversement proportionnels aux composantes.
appliquée en A. Deux forces parallèles inégales et de sens contraires ont une résultante parallèle de même sens que la plus grande, placée à l’extérieur des composantes, égale à leur différence ; la ligne d’action de cette résultante divise la droite joignant les points d’application des composantes en deux segments inversement proportionnels aux composantes.
• Cas de deux forces parallèles, égales et de sens contraires. Il s’agit d’un couple. Le point A est rejeté à l’infini. Le moment d’un couple est le même par rapport à tout point de l’espace.
• Cas de n forces parallèles  On remplacera
On remplacera  par leur résultante
par leur résultante 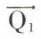 , que l’on composera avec
, que l’on composera avec  . On obtiendra une nouvelle résultante, que l’on composera avec
. On obtiendra une nouvelle résultante, que l’on composera avec  , et ainsi de suite. L’intensité de la résultante est la somme algébrique des intensités des composantes. La résultante, si elle est différente de zéro, est appliquée en un point O, qui est le centre des forces parallèles.
, et ainsi de suite. L’intensité de la résultante est la somme algébrique des intensités des composantes. La résultante, si elle est différente de zéro, est appliquée en un point O, qui est le centre des forces parallèles.

Centre de gravité
C’est le point du corps par lequel passe constamment la verticale de son poids, quelle que soit son orientation. C’est le centre des forces parallèles attachées à tous les points du corps.
Expression des coordonnées du centre de gravité d’un corps
Si m1, m2, ..., mn sont les masses des différents points matériels composant le corps, p1, p2, ..., pn leurs poids, x1, y1, z1, x2, y2, z2, ..., xn, yn, zn leurs coordonnées, les coordonnées x0, y0, z0 du centre de gravité seront
et, en appelant M la masse du corps, ces coordonnées x0, y0, z0 ont pour valeur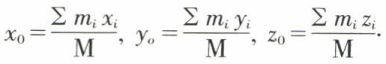
Théorèmes relatifs aux centres de gravité
• Quand un système matériel admet un centre de symétrie, son centre de gravité se confond avec son centre de symétrie.
• Quand un système matériel plan admet un diamètre rectiligne conjugué d’une direction de cordes, le centre de gravité du système est sur ce diamètre.
Un système plan admet un diamètre D conjugué d’une direction de cordes D′ quand on peut le diviser en couples d’éléments matériels A et B, tels que A ait même masse que B, que les cordes AB soient parallèles à D′ et qu’enfin leurs milieux soient sur D. Dans ce cas, le centre de gravité de chaque couple A et B est sur D. Le centre de gravité du système total y est aussi.
• Quand un système matériel admet un plan diamétral d’une certaine direction de cordes, le centre de gravité du système est dans ce plan.
Ce plan peut être divisé en couples d’éléments A et B de même masse ; les cordes AB sont parallèles à D′, et leurs milieux sont dans le plan P.
M. D.
➙ Dynamique / Mécanique / Vecteur.
P. Appell et J. Chappuis, Leçons de mécanique élémentaire (Gauthier-Villars, 1903 ; 3e éd., 1909, 2 vol.). / H. Bouasse, Cours de mécanique rationnelle et expérimentale (Delagrave, 1910) ; Statique (Delagrave, 1921). / M. Lecornu, Cours de mécanique professés à l’École polytechnique (Gauthier-Villars, 1914-1918 ; 3 vol.). / Soc. acad. Hütte, Des Ingenieurs Taschenbuch (Berlin, 1951-1955, 5 vol. ; trad. fr. Manuel de l’ingénieur, Béranger, 1960-192 ; 2 vol.).




