probabilité (suite)
Événements indépendants
A et B étant deux événements de probabilités non nulles, on dit que A est indépendant de B, relativement à P, si PB(A) = P(A).
Il en résulte alors que P(A ⋂ B) = P(A).P(B) et, par suite, que PA(B) = P(B). Les événements A et B sont alors indépendants, conformément à la définition plus générale suivante : deux événements A et B sont indépendants s’ils satisfont à la relation
P(A ⋂ B) = P(A).P(B).
Cette définition n’exclut pas les probabilités nulles. Si A et B sont indépendants, il en est de même de A et 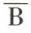 , de
, de  et B, et de
et B, et de  et
et 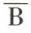 .
.
• Généralisation de la notion d’indépendance au cas de trois événements au moins. L’axiome des probabilités composées se généralise pour trois événements ; on a
P(A ⋂ B ⋂ C) = P(A).PA(B ⋂ C) = P(A).PA ⋂ B(C)
et d’autres égalités en permutant A, B et C. On dit que des événements sont totalement indépendants si les probabilités conditionnelles sont égales aux probabilités simples. Ainsi, pour trois événements A, B et C, on doit avoir
PB(A) = PC(A) = PB ⋂ C(A) = P(A)
et les égalités analogues.
Exemple. On jette deux dés cubiques dont les faces sont numérotées de 1 à 6. Soit les événements :
A, le premier dé montre une face impaire ;
B, le deuxième dé montre une face impaire ;
C, la somme des points obtenus est impaire.
L’univers est constitué de 36 couples ; |A| = |B| = |C| = 18, alors que
|A ⋂ B| = |B ⋂ C| = |C ⋂ A| = 9 ;
d’où les probabilités
Les événements A, B et C sont deux à deux indépendants, puisque l’on a 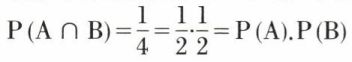 et les deux égalités analogues. Cependant,
et les deux égalités analogues. Cependant,
P(A ⋂ B ⋂ C) = 0 ≠ P(A).P(B).P(C).
Les événements A, B et C ne sont pas totalement indépendants : il manque une condition pour que l’indépendance totale soit réalisée.

E. S.
➙ Aléatoire (variable) / Binomiale (loi) / Comminatoire (analyse) / Gauss.
W. Feller, An Introduction to Probability Theory and its Applications, t. I (New York, 1950 ; nouv. éd., 1968). / H. Cramer, The Elements of Probability Theory and Some of its Applications (New York, 1955). / J. G. Kemeny, J. L. Snell et G. L. Thompson, Introduction to Finite Mathematics (Englewood Cliffs, N. J. 1957, 2e éd., 1966 ; trad. fr. Algèbre moderne et activités humaines, Dunod, 1959, nouv. éd., 1969). / B. V. Gnedenko et A. I. Kintchine, Introduction à la théorie des probabilités (trad. du russe, Dunod, 1960 ; nouv. éd., 1969). / P. Rosenstiehl et J. Mothes, Mathématiques de l’action (Dunod, 1965 ; nouv. éd., 1968). / G. Calot, Cours de calcul des probabilités (Dunod, 1967). / G. Letac, Problèmes de probabilité (P. U. F., 1970). / A. Jacquard, les Probabilités (P. U. F., coll. « Que sais-je ? », 1974).
Quelques grands noms de la théorie des probabilités
Jules Blenaymé
(Paris 1796 - id. 1878). Inspecteur général des Finances, il est connu en calcul des probabilités pour la découverte d’une inégalité fondamentale, appelée parfois inégalité de Bienaymé-Tchebychev. (Acad. des sc., 1852.)
Antoine Augustin Cournot.
V. l’article.
Pierre Simon, marquis de Laplace.
V. l’article.
Andreï Andreïevitch Markov
(Riazan 1856 - Leningrad 1922). Étudiant à l’université de Saint-Pétersbourg, il est reçu docteur en mathématiques en 1884. Privat-docent en 1880, membre de l’académie des sciences de Saint-Pétersbourg en 1890, il enseigne les mathématiques de 1886 à 1907. De 1899 à 1907, il édite les œuvres de son maître P. L. Tchebychev.
En 1891 parait son Calcul des différences finies et en 1900 son ouvrage fondamental sur le calcul des probabilités, qui eut une seconde édition en 1908. Le problème des probabilités en chaîne, suscité par Markov et Henri Poincaré, a été renouvelé par la méthode directe de Jacques Hadamard.
Abraham de Moivre
(Vitry-le-François 1667 - Londres 1754). Réfugié en Angleterre à la révocation de l’édit de Nantes (1685), il y passe la plus grande partie de sa vie. L’étude des Principes de Newton fait bientôt de lui un des premiers mathématiciens de son pays d’adoption, et il est élu membre de la Royal Society en 1697. Son ouvrage fondamental, paru en latin en 1711 (De mensura sortis), eut trois éditions anglaises (Doctrine of Chances) en 1718, en 1738 et en 1756. Jusqu’à Laplace, la théorie des probabilités lui doit plus qu’à tout autre mathématicien. Son nom est resté attaché à la formule
(cos x + i sin x)n = cos nx + i sin nx,
dont il est effectivement l’auteur, sous un aspect cependant assez différent. (Acad. des sc., 1754.)
Pierre Rémond de Montmort
(Paris 1678 - id. 1719). Fils d’un écuyer sieur de Bréviande, il refuse de poursuivre des études de droit et fuit la maison paternelle pour séjourner en Angleterre, aux Pays-Bas et en Allemagne. La lecture de la Recherche de la vérité fait de lui un disciple de Nicolas de Malebranche. Rentré en France en 1699, Montmort devient chanoine de Notre-Dame, mais abandonne cette dignité ecclésiastique à son frère et achète en 1704 la terre de Montmort.
Son Essai d’analyse sur les jeux de hasard a eu deux éditions, l’une en 1708, l’autre, très enrichie, en 1713. (Acad. des sc., 1716.)
Denis Poisson
(Pithiviers 1781 - Paris 1840). Fils d’un employé municipal de Pithiviers, il fait ses études à Fontainebleau et entre premier à l’École polytechnique en 1798. Après avoir remplacé dans sa chaire Joseph Fourier (1768-1830) pendant la campagne d’Égypte, il est nommé en 1806 professeur titulaire à l’École polytechnique puis, en 1809 professeur à la faculté des sciences de Paris dès sa fondation. Membre du Bureau des longitudes en 1808, membre de l’Institut en 1812, baron d’Empire, pair de France en 1837, il a la faveur de tous les régimes qui se sont succédé jusqu’à sa mort. Membre du Conseil royal de l’Instruction publique à partir de 1820, il eut une grande influence sur l’enseignement des mathématiques. Ses travaux personnels portent sur la mécanique céleste, l’électrostatique, le magnétisme et le calcul des probabilités, où son nom est resté attaché à la distribution de Poisson. (Acad. des sc., 1812.)




