probabilité (suite)

La probabilité ainsi définie vérifie les deux conditions de la définition, puisque

et si A et B sont deux événements incompatibles de , c’est-à-dire n’ayant aucune éventualité commune, le nombre de cas favorables correspondant à l’événement A ou B, noté A ∪ B, est la somme des nombres de cas favorables correspondant à A et à B ; on a donc bien
P(A ∪ B) = P(A) + P(B).
Dans le cas d’un univers fini, ce qui est souvent le cas, une probabilité est un rapport. Le problème de l’évaluation de ce rapport revient à deux dénombrements : celui des possibles et celui des cas favorables. On fait alors appel à l’analyse combinatoire. Mais ces dénombrements sont souvent source d’erreurs. Il est, en particulier, essentiel de bien préciser l’univers des possibles comme le montre l’exemple suivant.

• Exemple 2. Si on lance deux pièces indiscernables, quelle est la probabilité de les voir retomber sur deux côtés différents (pile P et face F) ?
Mauvaise réponse. Les pièces étant indiscernables, les seuls résultats que l’on peut voir sont PP, PF, FF ; l’univers des possibles est donc de cardinal 3 ; il y a un cas favorable, PF ; la probabilité cherchée est donc
Bonne réponse. Bien qu’indiscernables, les pièces peuvent être numérotées, ne fut-ce que mentalement, soit 1 et 2. Les différents résultats possibles sont, avec leur provenance

et les quatre résultats énumérés ont une existence ; ils constituent donc l’univers des possibles avec lequel il faut compter si l’on veut parier, par exemple.

Propriété des probabilités

1. L’application P est croissante : pour tout couple (A, B) d’événements tels que A ⊂ B, on a
P(A) ≤ P(B),
en particulier, si B = Ω,

En effet, comme A ⊂ B, on a
B = A ∪ (B – A),
les événements A et B – A étant incompatibles ; d’où

2. Pour tout couple d’événements (A, B), on a
P(A ∪ B) = P(A) + P(B) – P(A ⋂ B).
En effet,
P(A ∪ B) = P[A ∪ (B – A)] = P(A) + P(B – A)
et
P(B) = P[(B – A) ∪ (A ⋂ B)] = P(B – A) + P(A ⋂ B) ;
d’où l’égalité annoncée.
3. Pour tout événement A, Ā étant l’événement contraire, P(A) + P(Ā) = 1. En effet, P(A ∪ Ā) = P(Ā) + P(Ā) = P(Ω) = 1, Ω étant l’univers.
4. Pour toute famille finie d’événements deux à deux incompatibles, on trouve

Si la famille est un système complet d’événements, on a alors

On utilise pour cette quatrième propriété une démonstration par récurrence sur n.

Probabilité conditionnelle
Indépendance

En jetant un dé truqué à 6 faces, on estime que les faces peuvent sortir avec les probabilités suivantes :

On peut considérer les événements suivants :
A, le résultat obtenu est pair ;
B, le résultat est compris, au sens large, entre 2 et 5.

On calcule la probabilité pour que le résultat soit pair, sachant qu’il est compris entre 2 et 5. Cette probabilité est notée P_B(A) ; on lit « P de A sachant B » ou « P de A si B ». Elle est égale au quotient de la somme des probabilités des faces paires comprises entre 2 et 5 (c’est-à-dire 2 et 4) par la somme des probabilités des faces comprises entre 2 et 5 :

Cette nouvelle probabilité, par rapport à la probabilité P, correspond à un nouvel univers, {2, 3, 4, 5}, au lieu de {1, 2, 3, 4, 5, 6} ; ce nouvel univers est dû à une information supplémentaire : le résultat est compris entre 2 et 5. C’est la situation d’une personne qui, ayant joué les faces paires et étant loin de la table de jeu, ne connaît pas le résultat exact, mais qui déduit, d’après ce qu’elle entend autour d’elle, que le résultat est compris entre 2 et 5 ; elle se pose donc la question suivante : « Quelle est la probabilité pour que ce soit le 2 ou le 4 ? » Les probabilités conditionnelles sont fort importantes. Elles interviennent constamment au cours d’un problème de probabilités à mesure que se modifie l’information, donc l’univers.

Probabilité conditionnelle

Soit Ω un univers muni d’une probabilité P et B un événement de de probabilité non nulle. L’application de dans ℝ₊, qui à tout événement de associe le réel positif

est encore une probabilité sur Ω, appelée probabilité conditionnelle relative à B.

P_B(A) est la probabilité pour que A soit réalisé sachant que B est réalisé, ou probabilité conditionnelle de A relative à B.

On a

et, pour tout couple (A, A′) d’événements incompatibles,

Ainsi, les deux axiomes définissant une probabilité sont satisfaits, et P_B est bien une probabilité sur Ω.

• Propriétés des probabilités conditionnelles
1. Si B implique A, c’est-à-dire B ⊂ A, on a P_B(A) = 1 puisque

2. Pour tout couple (A, B) d’événements de probabilité non nulle, on a
P(A ⋂ B) = P(B) · P_B(A) = P(A) – P_A(B)
(formule dite « des probabilités composées »).
Ces deux égalités, qui proviennent des définitions de P_B(A) et de P_A(B), sont d’une extrême importance. Elles permettent de calculer la probabilité d’une intersection à l’aide d’une probabilité simple et d’une probabilité conditionnelle.
3. S’il existe un système complet d’événements pour tout événement A, on a (formule dite « des probabilités totales »).
Si P(A) ≠ 0, ∀_i ∈ [1, n],
(formule de Bayes ou formule de probabilité des causes, les événements B_i étant appelées causes).

L’événement A peut, en effet, s’écrire

et, comme les événements A ⋂ B_i sont deux à deux incompatibles, puisque les événements B_i le sont,

Il en résulte que
On utilise souvent la formule de Bayes dans le cas d’un système complet formé de deux événements : B₁ = B et événement contraire de B. On a alors

Exemple. Deux tireurs (a) et (b) tirent sur une même cible. Un observateur placé dans la fosse située au-dessous de la cible et qui ne voit pas les tireurs a l’opinion suivante : il estime que la carabine sera confiée au tireur (a) avec la probabilité 0,7 ; dans ce cas, le tireur (a) fait mouche avec la probabilité 0,9 ; si la carabine est confiée au tireur (b), celui-ci fait mouche avec la probabilité 0,4. Un projectile atteint la cible. Quelle est la probabilité, selon l’observateur, pour que ce soit (a) qui ait eu la carabine en mains ? Les possibilités sont les suivantes : A, la cible est atteinte ; , elle est ratée ; B, (a) a la carabine ; 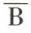, (b) a la carabine. On veut calculer P_A(B) et l’on a

les différentes probabilités intervenant dans ce calcul étant