pointes (pouvoir des) (suite)
Les apparences lumineuses et la stabilité du phénomène dépendent beaucoup de la polarité. Dans l’air, on observe en négatif un champignon bleu violacé, de petites dimensions (millimètre). La décharge est silencieuse et très stable. En positif, au contraire, on a des arborescences très ramifiées, qui s’étendent à une distance considérable de la pointe (plusieurs centimètres si elle est fine ; des décimètres si elle est grossière). On entend un bruit sifflant ou crépitant ; le phénomène est instable et tourne facilement en étincelle si la contre-électrode n’est pas très éloignée. Lorsque la pression est supérieure à quelques bars, il arrive que l’effluve positif disparaisse complètement : on n’observe plus que des étincelles.
Dans un liquide, il y a toujours, par rapport à un gaz, une grande abondance d’ions dus aux électrolytes dissous. Le champ intense au voisinage d’une pointe augmente de façon parfois très importante leur dissociation, et, d’autre part, des ions nouveaux sont formés à la surface de la pointe elle-même par des réactions électrochimiques. Ainsi, sans qu’aucune avalanche électronique n’ait lieu, la pointe et le liquide environnant réalisent encore une source d’ions unipolaires.
Toutefois, en raison de la nature essentiellement chimique du phénomène, la composition du liquide, celle des électrolytes et d’autres impuretés dissoutes jouent un rôle capital. La présence d’oxygène (qui donne des ions négatifs), d’eau (qui donne des protons), de traces d’autres corps facilement oxydables ou réductibles peut changer l’intensité du courant de plusieurs ordres de grandeur. Il n’y a d’ailleurs plus de seuil de tension défini, bien que le courant croisse encore très vile avec la tension.
En raison de la forte résistance opposée par le milieu aux ions, son entraînement est intense, et l’on observe une vive turbulence. Lorsque la tension et le courant sont assez élevés, la cavitation apparaît. Les bulles sont soumises à un champ électrique encore plus grand que le liquide (en raison des constantes diélectriques) et sont le siège de décharges lumineuses. Ces phénomènes, encore mal connus, jouent un rôle certain dans le claquage des liquides.
On a utilisé l’effet d’entraînement à la construction de « pompes ioniques », de modestes performances, mais d’une extrême simplicité.
L’effet de pointe a de très nombreuses applications, qui résultent de l’« écoulement » facile de l’électricité de la pointe soumise à une différence de potentiel de quelques kilovolts au moins. On s’en sert couramment pour communiquer à des objets une charge électrique sans contact, qu’il s’agisse de poussières, de brouillards de poudres (précipitation et projection électrostatiques) ou de surfaces solides isolantes (générateurs électrostatiques, xérographie). Les figures de Lichtenberg sont dues à la fixation, sur une surface isolante, des ions gazeux créés à son voisinage par une pointe.
On peut aussi (au moins partiellement) décharger un objet électrisé soit en le munissant de pointes, s’il est conducteur (avions), soit en disposant près de lui des pointes reliées au sol (industries textile et papetière). Le paratonnerre est, lui aussi, souvent cité ; en fait, il se borne à « attirer » la foudre en provoquant une décharge secondaire qui rejoint la décharge principale venant du nuage ; il est tout à fait incapable de neutraliser silencieusement un nuage orageux par son courant d’effluve, comme on l’affirmait encore au début du siècle, car ce courant, de quelques microampères, est négligeable vis-à-vis de celui qui charge le nuage (plusieurs ampères).
N. F.












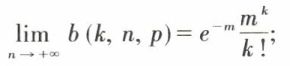
 est la probabilité pour qu’une variable aléatoire binomiale de paramètres n et p prenne la valeur k ; 0 < p < 1 ; n ∈ ℕ.
est la probabilité pour qu’une variable aléatoire binomiale de paramètres n et p prenne la valeur k ; 0 < p < 1 ; n ∈ ℕ.