isométrie
Application définie entre deux espaces affines euclidiens, telle que la distance entre les points images est la même qu'entre les antécédents correspondants. (On peut aussi définir l'isométrie affine dans un même espace affine comme application affine dont l'endomorphisme [ou isométrie vectorielle] associé est orthogonal. Si ce dernier est positif, on précise isométrie positive [ou isométrie directe ou déplacement] ; sinon, on parle d'isométrie négative [ou isométrie non directe].)
MATHÉMATIQUES
Parmi les isométries affines figurent les translations, dont l'endomorphisme associé est l'identité de l'espace vectoriel associé, et les rotations, dont l'endomorphisme associé est une rotation vectorielle. L'ensemble des isométries d'un espace affine E constitue, pour la loi de composition des applications, un groupe, noté Is(E), dont le groupe des déplacements ou isométries positives, est un des sous-groupes, noté Is+(E). Sur la droite affine, les isométries positives sont les translations et les isométries négatives les symétries par rapport à un point. Dans le plan affine, les isométries positives sont les translations et les rotations ; les isométries négatives sont les symétries orthogonales et les composées de ces symétries avec les translations. Dans l'espace affine E3, les isométries positives sont les vissages et les rotations ; les isométries négatives sont les composées d'une symétrie plane et d'une translation, les composées d'une symétrie plane et d'une rotation d'axe perpendiculaire au plan, les symétries centrales.
L'ensemble des isométries vectorielles d'un espace vectoriel euclidien
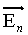 fini a une structure de groupe ; pour la composition des applications, c'est le groupe orthogonal de
fini a une structure de groupe ; pour la composition des applications, c'est le groupe orthogonal de
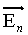 noté
noté
 , sous-groupe du groupe linéaire
, sous-groupe du groupe linéaire
 . Une isométrie vectorielle est une application linéaire bijective qui laisse invariant le produit scalaire de deux vecteurs, qui transforme toute base orthonormée de
. Une isométrie vectorielle est une application linéaire bijective qui laisse invariant le produit scalaire de deux vecteurs, qui transforme toute base orthonormée de
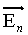 en une famille orthonormée, et qui conserve la norme de tout vecteur de En.
en une famille orthonormée, et qui conserve la norme de tout vecteur de En.
Dans un espace vectoriel de dimension 2, une isométrie est soit une rotation vectorielle, soit une symétrie orthogonale par rapport à une droite vectorielle. Dans un espace vectoriel de dimension 3, une isométrie est soit une symétrie par rapport à un plan, soit une rotation vectorielle ayant pour axe une droite vectorielle, soit la composée de 3 symétries orthogonales planes qu'on peut ramener à la composée d'une rotation vectorielle et d'une symétrie orthogonale vectorielle plane, l'axe de la rotation et le plan de la symétrie étant orthogonaux.
Dans toute base orthonormée, le déterminant d'une isométrie vectorielle est égal à 1 (isométrie positive) ou à − 1 (isométrie négative).



