espace vectoriel

Généralisation des espaces vectoriels de la géométrie.

MATHÉMATIQUES

Espace vectoriel

La structure d'espace vectoriel sur un corps K est une des notions de base de l'algèbre linéaire. En géométrie, un espace affine étant défini à partir d'un espace vectoriel, toute étude dans l'espace affine se ramène à une étude dans l'espace vectoriel associé. L'étude des espaces vectoriels dont les éléments sont des fonctions, munis d'une norme convenable, est devenue un des éléments essentiels de l'analyse. Les principaux exemples d'espaces vectoriels sont les ensembles formés des éléments suivants : les polynômes à une indéterminée, les matrices de type (n,p) sur un corps K ; les applications linéaires du K-espace vectoriel E dans le K-espace vectoriel F, les formes linéaires d'un K-espace vectoriel E.

Tout K-espace vectoriel E admet au moins deux sous-espaces vectoriels, le singleton { 0 } et E lui-même. L'ensemble de toutes les combinaisons linéaires finies d'éléments d'une partie A de E est un sous-espace vectoriel de E. Le sous-espace vectoriel F engendré par n éléments x₁, x₂, …, x_n de E est le sous-espace vectoriel des combinaisons linéaires de x₁, x₂, …, x_n ; on dit que x₁, x₂, …, x_n est une partie génératrice de F. Si l'espace E est lui-même engendré par un nombre fini de ses éléments, il est dit de dimension finie.

L'étude des applications linéaires entre deux espaces vectoriels de dimension finie à partir de leur base conduit au calcul matriciel, celle de la notion de forme multilinéaire à la théorie des déterminants et celle des formes linéaires d'un espace vectoriel aux notions de dual et de tenseur.

Espace vectoriel de dimension finie

Un espace vectoriel de dimension finie est un espace vectoriel engendré par un nombre fini de ses éléments.

Tout sous-espace vectoriel de E est aussi de dimension finie ou égale à celle de E. Si f est une application linéaire d'un K-espace vectoriel E dans un K-espace vectoriel F, alors la dimension de f(E) est finie et inférieure ou égale à celle de E ; elle définit le rang de f et

rg(f) = dim E − dim ker(f),

ker(f) désignant le noyau de f. Dans le cas où E et F ont la même dimension, les propriétés suivantes sont équivalentes : f est bijective, f est injective et f est surjective.

Dual d'un K-espace vectoriel E

Ensemble ℒ(E ; K) des formes linéaires définies de E dans K. (On le note E*.)

Si E est de dimension finie n, et si est de base E, alors E^* est aussi de dimension finie n. Une base de E^* est 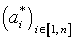où a_i* est défini par

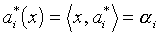
, avec .

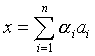Norme

Sur l'ensemble ℝ des réels en tant qu'espace vectoriel, l'application qui, à tout réel, associe sa valeur absolue est une norme. Sur l'ensemble ℂ des complexes, l'application qui, à tout complexe, associe son module est une norme. Tout espace muni d'une norme peut être muni d'une distance, plus particulièrement la distance définie par .