mécanique céleste (suite)

Pour trouver le mouvement du point M connaissant la force qui agit sur lui, il faut intégrer l’équation différentielle du second ordre (1). Si le vecteur est nul, le vecteur est nul et le mouvement est rectiligne et uniforme. Comme cas particulier, le point M peut être fixe. La mécanique s’occupe aussi des systèmes d’un nombre fini ou infini de points matériels (corps solides ou fluides).

• La mécanique céleste s’occupe du mouvement des astres. Les astres sont des corps plus ou moins sphériques dont les rayons sont extrêmement faibles par rapport aux distances qui les séparent, aussi la mécanique céleste considère les astres comme des points matériels. De plus, les forces mises en jeu sont uniquement les forces de gravitation définies par la loi de Newton : « Un point matériel A de masse m, exerce sur un point matériel B de masse m′ une force attractive dirigée le long de BA, de B vers A et dont la grandeur est proportionnelle au produit mm′ et inversement proportionnelle au carré de la distance AB. » En vertu du principe de l’action et de la réaction, énoncé également par Newton, le point matériel B exerce alors aussi sur le point matériel A une force attractive égale, mais de sens contraire. La mécanique céleste a connu de grands succès depuis près de trois siècles dans l’étude des mouvements des astres du système solaire (Soleil, planètes, Lune, satellites). En effet, le problème mathématique de l’intégration des équations du mouvement étant résolu, il faut pour connaître le mouvement d’un astre avoir sa position et sa vitesse à un instant donné, ce qui n’est faisable que si l’on a des observations précises de l’astre considéré. La relative proximité des astres du système solaire rend de telles observations possibles.

Le problème des deux corps

Le seul problème de mécanique céleste vraiment simple à résoudre est celui des deux corps. Celui-ci suppose en présence deux corps seulement, par exemple le Soleil et une planète. L’intégration de l’équation (1), dans laquelle le vecteur est la force de gravitation, permet d’aboutir à la conclusion suivante. Chaque corps décrit autour de l’autre une courbe plane appelée conique : ellipse, hyperbole, ou parabole. Si la trajectoire de l’un des corps autour de l’autre est une ellipse, le mouvement est périodique. Chaque planète P décrit autour du Soleil S une ellipse dont le Soleil est l’un des foyers, le second foyer S′ de l’ellipse ne jouant aucun rôle dans le mouvement. D’autre part, le rayon vecteur SP balaie des aires égales en des temps égaux. Cela signifie que le point P met le même temps pour aller de P₁ en P₂ que pour aller de en les aires SP₁P₂ et étant égales. La vitesse du point P est la plus grande quand il passe au point H (périhélie) et la plus faible quand il passe en H′ (aphélie). Enfin, si le mouvement se fait sur une ellipse, le mobile P met pour faire le tour de l’ellipse un certain temps T ; si a est le demi-grand axe de l’ellipse, on a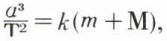

k étant une constante, m la masse du point P et M celle du point S. Si S est le Soleil et P une planète, m est très petit et, quelle que soit la planète, on pourra écrire :

Ces résultats sont connus sous le nom de lois de Kepler, car ils ont été découverts par Johannes Kepler* à partir de l’étude de la trajectoire de Mars. Ils ont été retrouvés par le calcul par Isaac Newton* à partir de la loi de la gravitation universelle.

Le problème de plusieurs corps

On peut facilement à partir de la relation (1) déterminer les équations du mouvement de plusieurs points matériels. Cependant, ces équations ont une structure mathématique tellement compliquée qu’il est impossible de les résoudre complètement, même s’il n’y a que trois corps en présence (c’est le fameux problème des trois corps). On se contente de rechercher une solution approchée des équations du mouvement compte tenu de certaines particularités de l’ensemble des corps étudiés. De ce fait, on est amené à distinguer plusieurs types de problèmes.

Théories planétaires

Les masses des planètes sont faibles par rapport à celle du Soleil, la plus élevée étant celle de Jupiter, qui est environ 1/1 000 de celle du Soleil ; on peut supposer qu’en première approximation une planète donnée a un mouvement képlérien autour du Soleil. Ce mouvement est entièrement défini par la donnée d’un certain nombre de constantes (six constantes), qui caractérisent la forme et la position de l’ellipse décrite dans l’espace. Si S est le Soleil, Sx et Sy deux axes situés dans un plan fixe, qui sera en général le plan de l’écliptique dans lequel se meut la Terre, l’orbite képlérienne d’une planète P est dans un plan qui fait l’angle i avec le plan xSy et qui coupe ce plan suivant la droite SN telle que Le périhélie étant le point H, l’angle sera appelé ω. On se donne également le demi-grand axe a, l’excentricité e de l’ellipse et enfin l’un des temps t₀, auquel le point P passe au périhélie. Si le mouvement était vraiment képlérien, les quantités i, Ω, ω, a, e, et t₀, appelées éléments elliptiques, auraient des valeurs constantes. Du fait de la présence des autres planètes, on considère que ces quantités sont égales à des constantes augmentées de certaines fonctions du temps que l’on cherche à déterminer par approximations successives à partir des équations du mouvement. Ces fonctions ont en facteur les masses des planètes perturbatrices, qui sont faibles. Les variations des « éléments elliptiques » sont d’amplitude très faible ou bien elles sont extrêmement lentes. Le demi-grand axe, l’excentricité et l’inclinaison varient périodiquement autour d’une valeur moyenne ; le point N (appelé nœud) et le périhélie font un tour complet autour de l’axe Sz, mais en un temps très long (plusieurs dizaines de milliers d’années en général). C’est grâce aux théories planétaires que Urbain Le Verrier (1811-1877) a découvert en 1846 la planète Neptune en analysant les perturbations d’origine inconnue que subissait Uranus.