Théorie mathématique édifiée dans la première moitié du xxe s. pour rendre compte de tous les phénomènes physiques microscopiques à l’échelle de l’atome.
Le nom de mécanique a été donné à cette théorie par analogie avec la mécanique rationnelle édifiée au xviiie s. pour rendre compte des mouvements des corps matériels, et à laquelle elle vient se substituer pour décrire les mouvements des corpuscules atomiques. Mais, pour l’opposer à la mécanique rationnelle, on la qualifie d’ondulatoire, ou de quantique ; le premier adjectif rappelle que cette théorie fait un large emprunt au formalisme mathématique de la théorie des ondes ; le second adjectif rappelle que cette théorie explique les phénomènes quantiques inexpliqués par la mécanique rationnelle.
Les termes quantique et quantification sont utilisés pour caractériser des grandeurs physiques dont on ne peut pas observer la variation continue et dont on mesure seulement des valeurs discontinues séparées par des quantités finies.
Historique
La première évidence d’un phénomène quantique est apparue au tout début de ce siècle dans l’étude du rayonnement thermique émis par une matière incandescente et elle a conduit à la notion de photon*. L’interprétation des spectres atomiques par Niels Bohr* en 1913 et les expériences d’excitation électronique effectuées la même année par James Franck et Gustav Hertz confirmèrent cette quantification de l’énergie et conduisirent à la notion de niveaux d’énergie quantifiés de l’atome. L’expérience effectuée en 1921 par Otto Stern et Walther Gerlach en envoyant un jet atomique à travers l’entrefer d’un aimant mit en évidence de manière irréfutable la quantification d’une autre grandeur physique : le moment cinétique.
Le formalisme mathématique de la mécanique rationnelle utilise des équations différentielles portant sur des fonctions continues et il est incapable de rendre compte des variations discontinues des grandeurs physiques. C’est Louis de Broglie* qui eut pour la première fois, en 1922, l’idée de substituer au formalisme de la mécanique classique celui de la théorie des ondes. Il fut guidé dans cette voie par la considération des phénomènes d’ondes stationnaires, où l’on observe les interférences entre une onde incidente et l’onde réfléchie (cordes vibrantes, tuyaux sonores, cavités résonnantes des ondes hertziennes). On sait que l’onde stationnais résultante prend une amplitude exceptionnellement importante pour certaines valeurs particulières de la longueur d’onde en accord avec les dimensions géométriques du dispositif vibrant ; les équations aux dérivées partielles de la théorie des ondes sont donc capables d’expliquer la quantification de certaines grandeurs. C’est ainsi que L. de Broglie fut conduit à associer au mouvement d’une particule de masse m et de vitesse v une onde dont la longueur d’onde λ est inversement proportionnelle à sa quantité de mouvement p = mv, soit 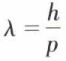 (h constante de Planck).
(h constante de Planck).
La mise au point du nouveau formalisme fut guidée par le double souci d’expliquer les résultats expérimentaux et de respecter le principe de correspondance énoncé par Bohr, et dont la signification est la suivante : bien que la nouvelle mécanique soit radicalement différente de la mécanique classique, lorsqu’on l’applique à des phénomènes à l’échelle atomique, elle doit au contraire conduire à des résultats identiques lorsqu’on l’applique à des phénomènes à notre échelle. Les résultats calculés par la mécanique quantique pour décrire un certain processus physique doivent tendre vers les résultats correspondants, calculés en mécanique classique, lorsque l’échelle des phénomènes devient importante ; c’est-à-dire lorsque les valeurs effectives des grandeurs physiques concernées deviennent très grandes devant les écarts entre valeurs quantifiées successives.
L’édification de la théorie quantique entrait dans sa phase décisive en 1925-1926 avec l’établissement simultané de la méthode de calcul des fonctions d’onde par Schrödinger* et de la méthode de calcul matriciel par Heisenberg*. Schrödinger réussissait aussitôt à montrer l’équivalence des deux méthodes de calcul apparemment très différentes. Le développement de la théorie s’effectuait alors très rapidement à la fois sur le plan mathématique avec les travaux de Max Born et Pascual Jordan, et sur le plan de la liaison avec l’expérience : interprétation probabiliste développée par Born en 1927 et par son élève Heisenberg avec le principe d’incertitude. Lorsque Paul Dirac* eut effectué en 1928 la synthèse de la nouvelle mécanique avec la théorie de la relativité, on put dire que la nouvelle mécanique était définitivement établie.





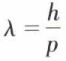 (h constante de Planck).
(h constante de Planck).