topologie (suite)

Sous-ensemble fermé d’un espace topologique E

On appelle ainsi toute partie complémentaire d’un ouvert de l’espace topologique E.

Les propriétés des fermés sont duales de celles des ouverts :
— l’ensemble E et l’ensemble vide sont fermés ;
— toute réunion finie de fermés est fermée ;
— toute intersection de fermés est fermée.

Dans ℝ, tout segment ou intervalle fermé est fermé : [a, b], formé des éléments x de ℝ tels que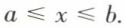

• Un point d’accumulation d’une partie A ⊂ E est un point x de l’espace E dont tout voisinage contient un point de A différent de x.

• Un point adhérent à une partie A ⊂ E est un point x de l’espace E tel que tout voisinage de x contient un point de A.

Un point adhérent à A est donc soit un point d’accumulation de A, soit un point isolé de A. Le point x = 1 est point d’accumulation de la partie A de ℝ formée des valeurs que prend quand n ∈ ℕ* et n → ∞ : quel que soit l’ouvert de centre 1 et de rayon ε, il existe n₀ ∈ ℕ*, tel que, pour n > n₀, |u_n – 1| < ε. La notion de point adhérent est liée à celle d’adhérence ou de fermeture.

Fermeture ou adhérence d’une partie A d’un espace topologique E

C’est le plus petit ensemble fermé contenant A, noté .

est l’intersection de toutes les parties fermées contenant A. Mais est aussi identique à l’ensemble des points adhérents à A. D’où la dénomination d’adhérence. Pour que la partie A soit fermée, il faut et il suffit que A contienne ses points d’accumulation. La relation caractérise les ensembles fermés. Il résulte de la définition de la fermeture que Enfin, si A ⊂ B, et, pour A et B quelconques,

Intérieur d’une partie A d’un espace topologique E

C’est le plus grand ouvert contenu dans A, noté Å.

La notion d’intérieur est duale de celle de fermeture. La relation A = Å caractérise les ouverts de l’espace E. On a 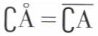et ces deux relations faisant la liaison entre intérieur et fermeture. Enfin, si A ⊂ B, 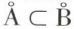et, pour A et B quelconques,

Frontière d’une partie A d’un espace topologique E

C’est la partie, notée A*, constituée des points dont tout voisinage contient au moins un point de A et un point de ∁a Ainsi, 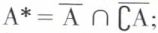A* est fermé puisque c’est l’intersection de deux fermés. De plus, 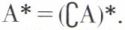Enfin, pour qu’un sous-ensemble fermé de E soit identique à sa frontière, il faut et il suffit qu’il ail son intérieur vide.

Exemples.

• Si E = ℝ, la fermeture de l’intervalle ]a, b[, ouvert, est l’intervalle fermé [a, b]. Les points a et b constituent la frontière de ]a, b[, qui est lui-même l’intérieur de [a, b].

• Si E = ℝ, l’intérieur de l’ensemble ℚ des rationnels est vide, car le seul ensemble ouvert contenu dans l’ensemble ℚ est l’ensemble vide. L’intérieur du complémentaire de l’ensemble ℚ dans l’ensemble ℝ a son intérieur vide aussi, ce complémentaire étant l’ensemble des nombres irrationnels. La frontière de l’ensemble ℚ est l’ensemble ℝ tout entier. Les deux sous-ensembles de l’ensemble ℝ, ℚ et ℝ – ℚ, complémentaires dans l’ensemble ℝ, sont tous deux non fermés et non ouverts. La fermeture de chacun d’eux est l’ensemble ℝ. Ainsi, tout point de l’ensemble ℝ est point d’accumulation de l’ensemble ℚ, par exemple. Cette propriété est en accord avec la possibilité de définir tout point de l’ensemble ℝ, c’est-à-dire tout nombre réel, par deux suites adjacentes de valeurs décimales approchées par défaut et par excès.

• Si E = ℝ et si A est une partie bornée de ℝ, la borne inférieure et la borne supérieure de A font partie de l’adhérence et de la frontière de A.

Partie A d’un espace topologique E, partout dense sur E

On appelle ainsi toute partie A de l’espace E telle que cela équivaut à dire que, dans tout ouvert de l’espace E, il y a des points de A.

L’ensemble ℚ des rationnels est partout dense dans l’ensemble ℚ : la fermeture de ℚ est ℝ.

On dira que A est non-dense sur l’espace E si l’intérieur de la fermeture de A est vide :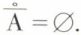

Si A est non-dense sur l’espace E, ∁a est partout dense. La réciproque est fausse.

Si A est partout dense dans l’espace E et si A ⊂ B ⊂ E, B est aussi partout dense sur l’espace E.

Si A et B sont non-denses, A ∪ B est aussi non-dense.

Ces dernières propriétés sont évidentes. Elles précisent, comme les définitions qui les précèdent, des notions intuitives telles que « dans l’ensemble des réels, il y a des rationnels partout » (l’ensemble ℚ est dense dans l’ensemble ℝ) ; cela est d’ailleurs en accord avec le résultat démontré et énoncé rigoureusement dans l’étude de la droite réelle : entre deux réels quelconques, il y a toujours un rationnel. L’ensemble ℚ fournit aussi un exemple de sous-ensemble de l’ensemble ℝ partout dense dans ℝ et dont le sous-ensemble complémentaire, ℝ – ℚ, non seulement n’est pas non-dense dans l’ensemble ℝ, mais est partout dense : il y a des réels irrationnels partout dans l’ensemble ℝ. D’ailleurs, toujours sous une forme intuitive, les irrationnels sont « plus nombreux » que les rationnels, car l’ensemble ℚ des rationnels est dénombrable, alors que l’ensemble ℝ a la puissance du continu et qu’il en est donc de même de ℝ – ℚ.

Ces remarques sont en accord avec les propriétés topologiques de ℝ, mais, plus que dans tout autre domaine des mathématiques, il faut se garder d’énoncer un résultat topologique fondé sur l’intuition : celui-ci sera toujours faux. Il ne faut pas, non plus, s’effrayer du langage : par exemple, ℚ et ℝ – ℚ ne sont ni ouverts ni fermés. De même, un espace topologique E et l’ensemble vide ∅ sont à la fois ouverts et fermés. Cela résulte de définitions précises et du vocabulaire choisi pour traduire telle ou telle propriété.