topologie (suite)

Espaces topologiques compacts

Un espace séparé est un espace vérifiant l’axiome de Hausdorff : deux points distincts ont deux voisinages distincts.

Un espace compact est un espace séparé E tel que, de tout recouvrement ouvert de cet espace, on puisse extraire un recouvrement fini.

Cela signifie que, si l’on peut recouvrir l’espace E par une famille d’ouverts (w_i) = i ∈ I, donc si il existe J ⊂ I, J fini, tel que

D’après le théorème de Borel-Lebesgue, tout intervalle fermé borné [a, b] de ℝ est compact. Les espaces compacts sont fort importants. Dans un espace compact, toute suite de points a au moins une valeur d’adhérence ; si une suite n’a qu’une valeur d’adhérence, la suite converge vers cette valeur. De façon plus générale, un espace compact vérifie une propriété analogue au théorème de Bolzano-Weierstrass pour la droite réelle : toute partie infinie a au moins un point d’accumulation.

Enfin, dans un espace compact, il y a identité entre les sous-ensembles fermés et les sous-ensembles compacts.

Une autre propriété que possèdent ℝ et tout intervalle de ℝ, la connexité, a conduit à définir de façon générale une autre classe d’espaces topologiques.

Espaces topologiques connexes

Un espace topologique E est dit connexe s’il n’existe aucune partition de cet espace en deux parties ouvertes (ou fermées) : on ne peut partager l’espace E en deux sous-ensembles non vides ouverts (ou fermés) : c’est ce que contient le mot partition. Il faut remarquer que cette définition n’est pas en désaccord avec l’axiome : l’espace E et l’ensemble vide ∅ sont ouverts (et fermés).

Partie connexe d’un espace topologique E

C’est une partie A de l’espace E telle que le sous-espace topologique A de l’espace E soit connexe, ce sous-espace topologique ayant pour ouverts les traces, sur A, des ouverts de l’espace E.

Tout intervalle de ℝ est connexe ; ℝ est connexe. En revanche, ℚ n’est pas connexe. En effet, la partie A de ℚ formée des nombres rationnels x tels que x² < 2 est identique à la partie de ℚ formée des nombres rationnels x tels que 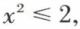puisque 2 n’est le carré d’aucun nombre rationnel. Donc A est à la fois ouvert et fermé. Sa partie complémentaire ∁a est donc aussi ouverte et fermée. On peut alors partager ℚ en A et en ∁a, tous deux non vides et ouverts. ℚ n’est pas connexe.

La fermeture de tout ensemble connexe est connexe, et la réunion d’une famille (A_i)_i ∈ I de parties connexes d’un espace topologique E, dont l’intersection n’est pas vide, est connexe.

Espaces métriques

Un espace métrique est le couple constitué par un ensemble E et une application d de E² dans ℝ, appelée distance, telle que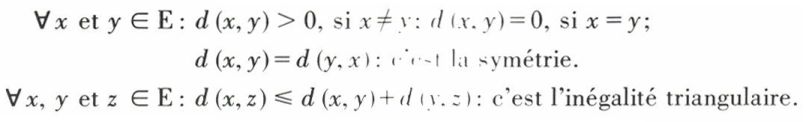

Métrique euclidienne. Dans l’espace ℝ″, on considère

Les deux propriétés concernant le signe et la symétrie de d sont vérifiées. La dernière propriété revient à vérifier que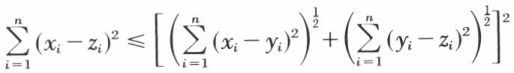

ou, en posant x_i – y_i = a_i, y_i – z_i = b_i et en remarquant que x_i – z_i = a_i + b_i, on a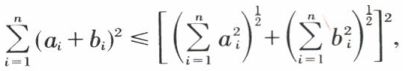

ou, en développant et en réduisant :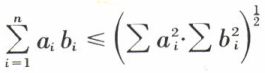

ou encore

ce qui résulte de l’identité de Lagrange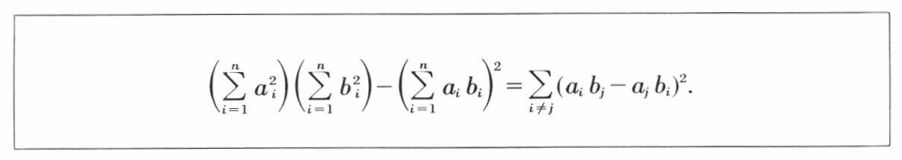

On peut définir sur un ensemble E muni d’une structure d’espace métrique une topologie directement liée à cette structure, c’est-à-dire liée à la distance définie sur cet ensemble E.

Boules d’un espace métrique

Dans un espace métrique E, une boule ouverte (resp. fermée) de centre a et de rayon ρ 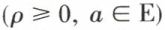est l’ensemble B (a, ρ) des points x de E tels que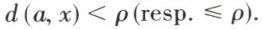

La sphère de centre a et de rayon ρ est l’ensemble S (a, ρ) des points x de E tels que d (a, x) = ρ.

Une partie A de l’espace métrique E, muni de la distance d, est ouverte si elle est vide ou si, pour tout point x de cette partie, il existe une boule ouverte de centre x, de rayon non nul et contenue dans cette partie A. Les « ouverts » ainsi définis vérifient les axiomes d’un espace topologique.

Toutes les définitions concernant les espaces topologiques s’appliquent aux espaces métriques, mais ces derniers possèdent des propriétés que ne vérifient pas nécessairement les espaces topologiques. Par exemple, tout espace métrique est séparé. Ou encore, pour qu’un espace métrique E soit compact, il faut et il suffit que toute partie infinie de cet espace ait un point d’accumulation : c’est dire que, dans un espace métrique, le théorème de Borel-Lebesgue est équivalent à celui de Bolzano-Weierstrass. On obtient ainsi une structure plus riche que celle d’espace topologique simple et conduisant à de nombreux résultats.

E. S.

➙ Continu (puissance du) / Espace euclidien de dimension trois / ℕ / Norme dans un espace vectoriel sur ℝ / ℚ / ℝ.

 H. Poincaré, Dernières Pensées (Flammarion, 1913). / P. S. Alexandroff, Elementary Concepts of Topology (en russe, Moscou, 1948 ; trad. angl., New York, 1961, 2^e éd., 1965). / S. Lefschetz, Introduction to Topology (Princeton, N. J., 1949). / A. H. Wallace, An Introduction to Algebraic Topology (Londres, 1957 ; trad. fr. Introduction à la topologie algébrique, Gauthier-Villars, 1973). / G. Choquet, Cours d’analyse, t. II : Topologie (Masson, 1964). / L. Chambadal et J. L. Ovaert, Cours de mathématiques, t. I : Notions fondamentales d’algèbre et d’analyse (Gauthier-Villars, 1966). / J. Lelong-Ferrand et J. M. Arnaudiès, Cours de mathématiques, t. II : Analyse (Dunod, 1972). / J.-C. Pont, la Topologie algébrique. Des origines à Poincaré (P. U. F., 1974).