systèmes formels

Systèmes de symboles, tels que l’on sait combiner les symboles entre eux, indépendamment de leur signification.

Systèmes formels ou langages formels

Pour résoudre le système des deux équations
x = 5 – y (1)
y + 4 = 7 (2)
il est possible de raisonner comme suit :
(a) Si on soustrait 4 aux deux membres de (2), alors y = 3.
(b) Si on remplace y par 3 dans (1), alors x = 2.

Le raisonnement qu’expriment les deux propositions (a) - (b) a pu se faire sans connaître la nature des grandeurs représentées par x et par y. Il exigeait, en revanche, de savoir ce que sont les « deux membres », ce que « soustraire » et « remplacer » veulent dire et de connaître la table de soustraction. Il est vrai que, dans le cas où ce fragment de la théorie des équations serait axiomatisé formellement (v. axiomatisation et formalisation), ce genre de connaissances ne serait plus requis. Il n’en resterait pas moins que les deux propositions (a) et (b) contiendraient encore l’expression française « si... alors ». On conçoit, toutefois, qu’en combinant une axiomatisation formelle avec un calcul logique (v. calcul des prédicats) il devienne possible de se libérer de tout appel à la signification des symboles. On sera en présence de suites de signes (x, y, 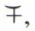, =, 5, ., ⊃, ∀, ∃, ...) dont chacune est engendrée par des règles bien définies et qui s’enchaînent selon d’autres règles bien définies. On dira que l’on a affaire à un langage formel ou encore à un système formel.

La notion de système formel

On peut donner à cette notion une généralité plus ou moins grande. Nous allons indiquer comment obtenir une classe de systèmes formels qui suffisent aux usages habituels.

1. On se donne d’abord un ensemble fini ou dénombrable de symboles quelconques. Notons-le a et nommons-le l’alphabet du système.

Il est possible de concevoir l’ensemble a* de toutes les chaînes finies que l’on peut écrire avec les éléments de a. Comme un même symbole peut se répéter aussi souvent qu’on le désire, a* est infini dénombrable, même si a est fini.

2. Si a était l’alphabet français, a* contiendrait aussi bien des suites qui forment un mot français que des suites qui n’en forment pas, comme bwk, arrx. Les mots français peuvent être considérés comme un sous-ensemble de a*.

Dans la construction d’un système formel, on introduit aussi un sous-ensemble e de a* qu’on appelle ensemble des expressions bien formées (ebf) ou encore ensemble des formules. Il y a toutefois ici une différence essentielle. Pour savoir si une suite de lettres est un mot français, il faut recourir au dictionnaire. D’autre part, certains dictionnaires peuvent accepter un mot, d’autres pas. L’ensemble e des ebf d’un système formel doit être engendré par des règles, dites règles de formation, d’une nature telle que l’on puisse décider par un procédé fini si une chaîne donnée quelconque est ou n’est pas élément de e. On dit alors parfois que e est un ensemble récursif.

3. On détermine ensuite un sous-ensemble de e, lui aussi récursif et que l’on nomme ensemble des axiomes. Désignons-le par s.

4. Donnons-nous enfin un ensemble fini r de règles, dites règles de déduction, qui permettent de passer de certaines ebf à d’autres ebf.

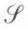Dans ces conditions, le quadruple est un système formel, et l’on appellera théorèmes de ou encore thèses de 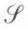l’ensemble t des ebf que l’on peut obtenir par les règles de r à partir des seuls éléments de s (à partir des axiomes).

On a donc s ⊂ e ⊂ a* et t ⊂ e.

Remarquons encore que, en général, t n’est pas un ensemble récursif ; il est seulement, comme on dit, engendré récursivement. Cela revient à affirmer que, si l’on sait toujours décider, devant une suite d’ebf, si celles-ci résultent les unes des autres par les règles de r, il se peut qu’on ne puisse décider si une ebf donnée est ou n’est pas un théorème (un élément de t).

L’exemple très simple suivant permettra de préciser la nature des règles de formation. L’alphabet est constitué de trois symboles :

La détermination de e comporte deux étapes :
(1) définition d’un ensemble récursif auxiliaire n/s ; et
(2) définition de l’ensemble récursif e.
(1) L’ensemble n est défini comme suit :
(a)  est élément de n.
(b) Si n est élément de n, 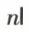est élément de n.
(c) Rien n’est élément de n, sinon par (a) et (b).

Il s’ensuit que les suites de « lettres » suivantes sont éléments de n : , , , , etc.

La définition ci-dessus comporte trois sortes de clauses :
(a) est une clause initiale. Elle énumère des éléments de l’ensemble (ici un seul).
(b) est une clause inductive. Elle indique comment engendrer un nouvel élément de l’ensemble à partir d’éléments déjà connus.
(c) est la clause finale. C’est elle qui permet de décider que la suite par exemple, n’est pas élément de n.

Les définitions de cette nature sont dites définitions inductives, parfois définitions récursives.

Une nouvelle définition inductive permettra d’engendrer e :
(a) Si n et m sont éléments de n, n * m est élément de e.
(b) Rien n’est élément de e, sinon par (a).
On notera que les clauses initiales peuvent manquer.

L’ensemble s est souvent un ensemble fini. Nous allons le choisir aussi simple que possible et poser

Nous construisons donc un système formel qui ne comporte qu’un seul axiome.