systèmes formels (suite)

L’ensemble r des règles est — dans notre définition — toujours fini. Nous n’en prendrons qu’une seule :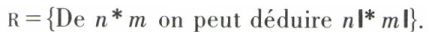

Dès lors, si l’on admet que tout élément de s est aussi un élément de t, les quatre ebf suivantes sont éléments de t, donc des théorèmes de ce système formel :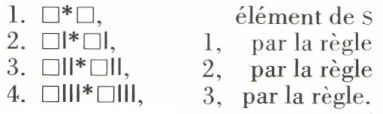

On voit, intuitivement, que tous les théorèmes auront la forme suivante :
un carré suivi de k barres, une étoile, un carré suivi de k barres.
Si l’on donne une démonstration de ce fait, on aura obtenu un théorème sur le système. Pour éviter de confondre les théorèmes, éléments de t, et les théorèmes qui énoncent des propriétés du système, nous appellerons ces derniers des métathéorèmes. Certains disent des épithéorèmes.

Il faut encore noter que, pour construire un système formel, on est dans l’obligation de faire usage d’une langue qui n’est pas celle que l’on élabore. La chose se marque clairement à propos des définitions inductives. Si, à la rigueur, la clause initiale qui définit n peut s’écrire simplement

il est impossible d’énoncer la clause (b) sans faire usage de la lettre n, qui n’appartient pas au système que l’on veut construire. On en conclut que la construction d’une langue formelle exige le recours à une autre langue, que l’on appelle alors métalangue (par rapport à cette langue).

Il en va de même pour l’énoncé et pour la démonstration des métathéorèmes. On peut, évidemment, se demander si on ne pourrait pas construire une langue formelle 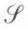assez riche pour qu’il soit possible, après coup, de l’utiliser pour « dire » ses propriétés. La réponse est toutefois négative (v. métamathématique).

Un système formel n’a d’intérêt épistémologique (n’apprend quelque chose sur la connaissance) que s’il est possible de l’interpréter. Donnons donc une interprétation au système ci-dessus et, pour cela, faisons correspondre :
le nombre zéro à ,
le suivant de à ,
est égal à *.
On voit alors que les éléments de n sont les nombres naturels 0, 1, 2, 3, ..., qu’une ebf est une égalité (vraie ou fausse) : n = m et que les théorèmes sont les égalités : 0 = 0, 1 = 1, 2 = 2, etc. Toutes ces égalités sont arithmétiquement vraies, et l’on dit que l’interprétation est un modèle (v. métamathématique).

Les systèmes combinatoires

En exigeant que, dans ce que nous avons appelé un système formel, a soit au plus dénombrable, que e et s soient des ensembles récursifs et que r soit fini, nous avons déjà limité la classe imaginable des systèmes formels. On peut, évidemment, s’imposer d’autres restrictions encore et définir ainsi des familles plus spéciales de systèmes formels. L’une d’elles, celle des systèmes dits combinatoires, offre un intérêt tout particulier.

Soit 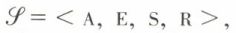où l’on a les conditions supplémentaires suivantes :
(1) a est un ensemble fini ;
(2) e = a* ;
(3) s n’a qu’un seul élément.
Dans ce cas, 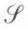est un système combinatoire.

On peut distinguer toutes sortes de variantes selon la nature des règles de déduction de 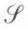. Nous allons nous contenter de celle où les règles ont la forme qui va être décrite.

Imaginons un alphabet a = {a, b, c}. Alors, les suites abaacb, aacb, abaa, aa sont éléments de a* et donc ici de e. Elles sont de la forme YXZ en appelant, par exemple, Y la suite ab, X la suite aa et Z la suite cb. Dans le deuxième exemple, Y est vide ; c’est X qui est vide dans le troisième, et, dans le quatrième, Y et Z sont toutes deux vides. Au lieu d’énoncer la règle « l’ebf U se récrit V », notons plus simplement : U → V.

Cela étant précisé, toutes les règles que nous allons considérer seront de la forme :
YXZ → YX′Z,
où X n’est pas vide.
Cela revient à donner des règles qui autorisent à remplacer un fragment de suite X par un autre X′, où qu’il se trouve dans une chaîne. Cela étant admis, on pourra écrire la règle ci-dessus plus simplement :
X → X′.

Exemple

a = {a, b, c}.
s = {c}.
R₁ : c → acb.
R₂ : c → ab.
On obtiendra des théorèmes en partant de l’axiome unique et en appliquant, au choix et si l’on peut, l’une des deux règles. Par exemple,
c → acb → aacbb → aaabbb
sont alors obtenus en appliquant deux fois R₁, puis R₂. Le dernier théorème ne permet plus d’en obtenir de nouveaux.

Remarque

Les théorèmes d’un système combinatoire sont souvent appelés ses productions.

On constate que, dans l’exemple ci-dessus, c joue un rôle particulier : tant qu’il figure dans une production, il est possible d’appliquer une des règles. De là l’idée de considérer deux parties dans l’alphabet, l’une, v_A, appelée vocabulaire auxiliaire et qui, ici, contient le seul symbole c, et l’autre, complémentaire, v_T, appelée vocabulaire terminal.

Soit alors un système combinatoire du genre considéré et tel que :
(1) a = v_T ∪ v_A ;
(2) l’axiome est élément de v_A ;
(3) les règles sont de la forme x → X, où x ∈ v_A et X ∈ a*, et où donc x est un et un seul symbole du vocabulaire auxiliaire et X une ebf quelconque. Un tel système est appelé une grammaire de Chomsky, et celles de ses productions (de ses théorèmes) qui ne comportent que des symboles du vocabulaire terminal le langage de Chomsky, associé à la grammaire.

Le système combinatoire ci-dessus est une grammaire de Chomsky si l’on pose
a = v_T ∪ v_A = {a, b} ∪ {c},
et le langage correspondant comprend les productions ab, aabb, aaabbb, etc.

Cette terminologie s’explique par l’usage particulier que Chomsky a fait de ces systèmes combinatoires. Soit, par exemple, le système suivant :
a = v_T ∪ v_A = {la, peur, guerre, engendre} ∪ {a, b, c, d, e, f}
s = {f}
R₁ : f → ab
R₂ : a → de
R₃ : b → ca
R₄ : c → engendre
R₅ : d → la
R₆ : e → peur
R₇ : e → guerre

Cette grammaire de Chomsky engendre un langage à quatre éléments :
f → ab → deb → deca → decde

Il est particulièrement éclairant de représenter les productions par des arbres. On aura ainsi pour la production (1) le schéma suivant.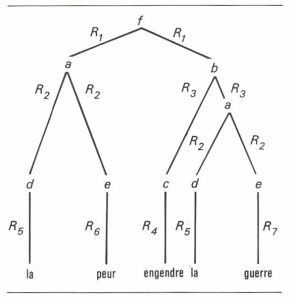

J.-B. G.

➙ Axiomatisation et formalisation / Chomsky / Générative (grammaire) / Langages formels.