instant

Cet article est extrait de l'ouvrage Larousse « Dictionnaire de la philosophie ».

Philosophie Antique, Philosophie des Sciences, Histoire des Sciences

Très petit espace de temps ; moment présent.

Aristote part de l'expérience du temps, celle qui se donne dans le mouvement uniforme du ciel, tout comme celle qui accompagne tout mouvement, dont on dit à juste titre qu'il prend un certain temps pour s'effectuer. Aristote se heurte aux apories du temps. Ces dernières révèlent le caractère impensable du temps, saisi nécessairement par le recours au moyen indirect de son expérience. Ce qui est le plus difficilement pensable, c'est le statut de l'instant, to nun. Celui-ci est limite, bordure entre passé et futur ; il n'est donc pas analysable en termes de substance. La question ontologique générale cède le pas à l'apode même de l'instant, puisqu'on ne peut construire de l'être à partir de ce qui n'est pas. Cette problématique de la substance rejoint celle de la réalité du temps et atteint, à coup sûr, le problème de la mesure du temps, puisque c'est à partir d'une compréhension du temps comme succession d'instants qu'on peut accéder à la mesure. Temps et mouvement se mesurent l'un l'autre, même si cette opération ne se fait pas de façon symétrique.

Le temps n'est donc pas substantialisable à partir de l'instant (ou du « maintenant ») considéré comme partie. C'est ici que s'infléchit, sans pour autant se dissoudre, l'orientation ontologique de l'investigation aristotélicienne. Si le maintenant semble bien posséder une certaine épaisseur d'être, celle-ci n'est pas généralisable, car ni le futur ni le passé ne possèdent (selon leur notion commune⁽¹⁾) de réalité. Mais ce n'est pas un défaut du présent / instant que de tendre à ce statut de simple limite tout en demeurant essentiellement quelque chose d'assignable. C'est, en effet, le seul moyen mis à notre disposition pour pouvoir encore parler du temps. Si le maintenant n'est rien, alors le temps n'a pas d'être, lui non plus. Si le maintenant dure, persiste, alors il n'y a pas de temps, mais une éternité immobile, une éternelle présence à soi où toutes les parties du temps sont pensées ensemble. L'instant est impensable, parce qu'il ne peut ni être dit néant ni être dit être. La seule façon de penser le temps, de lui donner hecceïté et forme est de le constituer à partir de l'analyse de la façon dont il accompagne le mouvement et la perception que nous en avons, la façon dont il est donné avec ou est « quelque chose » du mouvement (ti tes kineseos), la façon dont il est le nombre et est nombre par lui.

Il y aurait donc deux façons de thématiser le temps⁽²⁾, soit comme une successivité divisible en instants (on échappe à la régression par la convention : un instant est défini par telle périodicité), soit comme un donné qualitativement homogène en toutes ses parties, cadre où s'effectue une certaine quantité de mouvement.

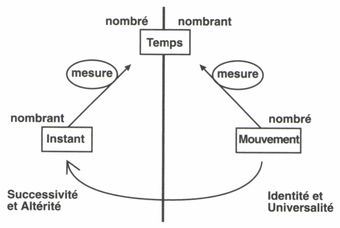
Le temps peut donc mesurer le mouvement et être mesuré par lui. C'est alors le mouvement qui est choisi comme unité mesurante (par excellence, le mouvement circulaire, mais, par extension, tout mouvement régulier, périodique, que l'on trouvera dans la nature ou dans l'artifice). Cette déréalisation de l'instant, par rapport aux parties du temps, est exactement celle à laquelle on aboutira lorsque viendra le temps de poser la question suivante : que deviennent les paramètres ordinaires du mouvement lorsqu'on les saisit dans un instant ? L'une des réalisations les plus difficiles de la mécanique classique fut de parvenir à construire la définition, puis la mesure d'un déplacement, d'une vitesse, d'une accélération dans un instant⁽³⁾. Mathématiquement, l'opération se trouva grandement simplifiée par l'invention d'un outil de dérivation continue et linéaire : le calculus leibnizien ou le calcul des fluxions newtonien, au xvii^e s., ont permis que soit élaboré un véritable algorithme de la cinématique par Varignon⁽⁴⁾. Physiquement, une grandeur instantanée demeure inscrite dans le cadre conceptuel forgé par Aristote, puisque l'opération de mesure du temps dans et par le mouvement aboutit, chez les physiciens classiques, à l'expression d'une tendance, d'un effort exprimé dans un nombre, que l'on ne saurait confondre avec la réalité qui s'y trouve nombrée.

Fabien Chareix

→ aristotélisme, mécanique, mouvement, temps