ℕ (suite)

• Étant donné deux entiers naturels non nuls a et b, il existe un nombre m multiple commun à a et à b, et tel que les multiples communs à a et à b soient les multiples de m (il y en a donc une infinité) ; m est le plus petit multiple commun, p. p. m. c. en abrégé, noté p. p. m. c. (a, b) ou a ∪ b ou a ∨ b. On a ab = md avec m = a ∪ b et d = a ∩ b ; il résulte de cette égalité que, si a et b sont premiers entre eux, a ∩ b = d = 1, m = ab : le p. p. m. c. de a et b est égal au produit de ces deux nombres. De façon générale, on obtient le p. p. m. c. de deux nombres a et b en faisant le produit des facteurs communs ou non communs figurant dans les décompositions de a et b en produits de facteurs premiers et en affectant chacun de ces facteurs du plus fort exposant. Si on multiplie (ou divise, si c’est possible) deux entiers naturels par un même nombre k, le p. p. m. c. des entiers ainsi obtenus s’obtient en multipliant l’ancien p. p. m. c. par k (ou en divisant).

Pour qu’un multiple commun à a et à b, M, soit le p. p. m. c. de a et de b, il faut et il suffit que c’est-à-dire que et 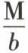soient premiers entre eux.

• Étant donné plusieurs entiers naturels en nombre au moins égal à trois, il existe un nombre m qui est le p. p. m. c. à ces nombres ; les multiples communs à ces entiers naturels sont les multiples de m (en nombre infini). Les propriétés énoncées pour le p. p. m. c. de deux entiers naturels s’étendent au cas d’un nombre fini quelconque d’entiers naturels.

• Caractères de divisibilité
Les caractères les plus usuels sont les caractères de divisibilité par 2 et 5, 4 et 25, 3 et 9 et 11. Pour établir ces caractères, on fait appel aux congruences arithmétiques. Un nombre est divisible :
— par 2 si et seulement s’il se termine par 0, 2, 4, 6, 8 ;
— par 5 s’il se termine par 0 ou 5 ;
— par 4 s’il se termine par 00, 04, 08, 12, 16, ..., 92, 96 (suite que l’on peut réduire à ses cinq premiers nombres en retranchant un multiple convenable de 20) ;
— par 25 s’il se termine par 00, 25, 50 ou 75.

• Reste de la division d’un nombre par 3 ou par 9. Le nombre écrit dans le système décimal est en fait égal à
a = u_n . 10ⁿ + u_n–1 . 10^n–1 + ... +
+ u₂ . 10² + u₁ . 10 + u₀.
Comme 10 = 9 + 1 = 3 × 3 + 1, 10 est « congru à 1 modulo 9 et modulo 3 », ce que l’on note :
10 ≡ 1(3) et 10 ≡ 1(9) ;
par suite, 10^k ≡ 1(3) ou (9),
d’où u_k . 10^k ≡ u_k,
d’où a ≡ u_n + u_n–1 + ... + u₂ + u₁ + u₀ :
le reste de la division par 9 ou 3 d’un nombre a, écrit dans le système décimal, est égal au reste de la division de la somme des chiffres de ce nombre.

• Caractères de divisibilité par 3 ou par 9. Pour qu’un nombre soit divisible par 3 ou par 9, il faut et il suffit que la somme de ses chiffres soit divisible respectivement par 3 ou par 9.

• Caractère de divisibilité par 11. Pour qu’un nombre soit divisible par 11, il faut et il suffit que la somme des chiffres de rang pair et la somme des chiffres de rang impair soient congrues modulo 11.

Exemple :
a = 5 467 883 014 est divisible par 11,
car 5 + 6 + 8 + 3 + 1 ≡ 4 + 7 + 8 + 0 + 4 ≡ 1 (11).

Nombres premiers

La suite des nombres premiers est infinie.

En effet, les nombres 2, 3, 5, 7, 11, ... sont premiers. Soit p le plus grand nombre premier connu et soit a = 2 × 3 × 5 × ... × p + 1 le nombre 2 × 3 × 5 × ... × p étant le produit de tous les nombres premiers connus inférieurs ou égaux à p ; a > p ; si a est premier, on a montré l’existence d’un nombre premier supérieur à p ; si a n’est pas premier, il admet un diviseur premier p′ qui ne peut être égal ni à 2, ni à 3, etc., ni à p, car, sinon, p′, divisant a et le produit 2 × 3 × ... × p, devrait diviser leur différence 1, ce qui est impossible ; donc p′ > p, ce qui montre l’existence d’un nombre premier supérieur à p. Ainsi, on trouve indéfiniment des nombres premiers, mais ils se raréfient à mesure que l’on atteint les nombres de plus en plus grands. La quantité de nombres premiers inférieurs à x tend vers quand x tend vers l’infini tout en restant entier, ce qui est en accord avec le fait qu’il existe une infinité de nombres premiers, puisque tend vers l’infini quand x tend vers l’infini (x entier ou non). En revanche, si quand représentant en quelque sorte la densité de nombres premiers au voisinage de x ou encore la probabilité pour x d’être premier. Cette probabilité tend vers zéro avec D’ailleurs, il existe des intervalles de l’ensemble ℕ aussi grands que l’on veut où on ne trouve aucun nombre premier.

Exemple :
a_n = (n + 1)! + 1 est tantôt premier (n = 2), tantôt composé (n = 3). Mais les nombres
(n + 1)! + 2, (n + 1)! + 3, ..., (n + 1)! + n + 1
sont tous composés, car ils sont respectivement divisibles (au moins) par 2, 3, ..., n + 1. On a ainsi une suite de n nombres tous composés ; n peut être choisi aussi grand que l’on veut, par exemple un milliard, ce qui peut paraître extravagant, car on imagine difficilement (n + 1)! dans ce cas. Le domaine mystérieux du nombre est plein de propriétés étranges, quelquefois démontrées, d’autres fois conjecturées et bien souvent inconnues.

E. S.

➙ Algébrique sur un anneau commutatif (équation) / Anneau / Axiomatique (méthode) / Combinatoire (analyse) / Continu (puissance du) / ℚ / ℝ / ℤ.

 A. Chatelet, Arithmétique et algèbre modernes (P. U. F., 1954-1966 ; 3 vol.). / J. Itard, Arithmétique et théorie des nombres (P. U. F., coll. « Que sais-je ? », 1964 ; 3^e éd., 1973) ; les Nombres premiers (P. U. F., coll. « Que sais-je ? », 1969). / O. Ore, Initiation to Number Theory (New York, 1966 ; trad. fr. Initiation à la théorie des nombres, Dunod, 1970). / C. S. Ogilvy et J. T. Anderson, Excursions in Number Theory (New York, 1969 ; trad. fr. Excursions dans la théorie des nombres, Dunod, 1970).