application (suite)

Qualités éventuelles

Injection ou application injective

C’est une application f : A → B pour laquelle tout élément de B est au plus une fois image. Sur la figure 4, on a le schéma d’une injection : sur un élément quelconque de B arrive au plus une flèche. Les applications définies par les figures 1 et 2 ne sont pas des injections.

Exemple. L’application f : ℝ⁺ → ℝ⁺ définie par est une injection de l’ensemble des réels non négatifs dans lui-même, car l’égalité x² = x′², qui est équivalente à
x² – x′² = 0 ou à (x – x′) . (x + x′) = 0,
n’est vérifiée que pour x = x′. Ainsi, les nombres x et x′ n’ont même image que s’ils sont égaux. De façon générale, f : A → B est une injection si, et seulement si, l’égalité f(x) = f(x′) n’est possible que pour x = x′.

Surjection ou application surjective

C’est une application f : A → B dans laquelle tout élément de B est au moins une fois image. Le schéma de la figure 5 est celui d’une surjection : sur chaque élément de B arrive au moins une flèche. La figure 1 ne montre pas une surjection, bien qu’il y ait deux flèches arrivant sur un élément particulier, car il y a trois éléments de B qui ne sont pas images.

Exemple. L’application f : ℝ⁺ → ℝ⁺ définie par est une surjection de ℝ⁺ dans ℝ⁺, car, quel que soit le nombre non négatif y, il existe un nombre réel non négatif, x, tel que y = x² : c’est le nombre . L’application f : ℝ → ℝ⁺ telle que est aussi une surjection de ℝ dans ℝ⁺. Pour une surjection, on peut parler d’une application d’un ensemble sur un autre, et non plus dans un autre.

Bijection ou application bijective

C’est une application à la fois injective et surjective. Le schéma de la figure 6 est celui d’une bijection : sur tout élément de B arrive une flèche et une seule. Les figures 1 et 2 n’indiquent pas des applications bijectives.

Exemple. L’application f : ℝ → ℝ définie par est une bijection de l’ensemble ℝ des réels dans lui-même. En effet, l’égalité x³ = x′³ est équivalente à
x³ – x′³ = 0, ou (x – x′)(x² + xx′ + x′²) = 0,
qui n’est vérifiée que pour x = x′, car le trinôme en x (ou en x′)
x² + xx′+ x′²
n’a pas de racines réelles.

Quand les ensembles A et B sont finis, ce qui est le cas dans toutes les figures utilisées jusqu’ici, il y a des relations nécessaires et suffisantes entre les cardinaux de ces ensembles (nombre d’éléments de ces ensembles) pour qu’il existe des injections, des surjections ou des bijections de A dans B (card. de A noté | A |) : a) injection, b) surjection, c) bijection, | A | = | B |.

Application inverse ou réciproque d’une bijection

Une bijection f : A → B associe à tout élément x de A un élément y de B et un seul. On définit alors l’application φ : B → A comme suit : x = φ(y) si, et seulement si, y = f(x) ; l’application φ est notée f^–1 et appelée application inverse, ou réciproque, de l’application f. Ainsi x = f^–1(y) si, et seulement si, y = f(x).

Exemples.

1. L’application inverse de f telle que de ℝ⁺ dans ℝ⁺, est définie par

en utilisant la même variable x.

2. Si f et f^–1 sont deux applications de ℝ dans ℝ.

Composition des applications

Opération que l’on peut définir quand on a trois ensembles A, B et C, non nécessairement distincts, une application f : A → B et une application g : B → C. Aux deux applications f et g (fig. 7), on associe une troisième h : A → C, définie comme suit : si x ∈ A et y = f(x), y ∈ B ; si z = g(y), alors z = h(x) ; l’application h est dite « composée » de f par g, et l’on note h = g ∘ f (g rond f), car z = g(y) ; mais y = f(x), d’où z = g[f(x)], que l’on note z = g ∘ f(x).

Exemple. Les trois ensembles A, B et C sont confondus avec l’ensemble ℝ des nombres réels ; f et g sont définies par et 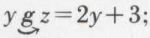alors,
z = g[f(x)] = 2(x² – 1) + 3 = 2x² + 1.
La fonction h est alors définie par

C’est une application de ℝ dans ℝ.

Propriétés de la composition des applications

• Associativité. On a quatre ensembles A, B, C, D et trois applications : f : A → B ; g : B → C et h : C → D ; pour tout élément x de A, il existe un élément y appartenant à B, tel que y = f(x) ; puis un élément z appartenant à C, tel que z = g(y) ; enfin un élément t appartenant à D, tel que t = h(z). Il existe donc une application φ : A → D telle que t = φ(x). Le schéma de la figure 8, où α = g ∘ f et β = h ∘ g sont deux applications composées telles que α : A → C et β : B → D, montre que t = h ∘ α(x) ou que t = β ∘ f(x) et que, par suite,
φ(x) = h ∘ α(x) = β ∘ f(x).
Les deux applications de A dans D, h ∘ α et β ∘ f, sont donc égales, et l’on peut écrire
φ = h ∘ α = β ∘ f,
ou encore
h ∘ (g ∘ f) = (h ∘ g) ∘ f.
Cette relation traduit l’associativité de l’opération composition des applications. On écrira φ = h ∘ g ∘ f.

• Revenons au cas de trois ensembles, A, B et C, que nous supposons ici confondus ; f : A → A et g : A → A. On peut définir f ∘ g aussi bien que g ∘ f ; y = f(x), z = g(y) ; y′ = g(x), z′ = f(y′) [fig. 9].

En général, z et z′ sont distincts, et, par suite,
f ∘ g ≠ g ∘ f.
Mais il peut arriver que
f ∘ g(x) = g ∘ f(x)
pour tout x de A ; alors
f ∘ g = g ∘ f,
et l’on dit que les deux applications f et g commutent.

Exemple.
A = ℝ, on vérifie la commutativité car
f ∘ g(x) = g ∘ f(x) = 32x⁶ – 48x⁴ + 18x² – 1.

• Application identique d’un ensemble A. C’est l’application I_A : A → A telle que I_A(x) = x, quel que soit l’élément x de A. Par suite, pour toute application f : A → B et pour tout élément x de A,
f ∘ I_A(x) = f[I_A(x)] = f(x), et f ∘ I_A = f,
B étant un ensemble quelconque.

De même, si g : C → A, C étant un ensemble quelconque, quel que soit l’élément x de A,
I_A ∘ g(x) = I_A[g(x)] = g(x),
et, par suite, I_A ∘ g = g.