magnétostatique (suite)

L’objet de la magnétostatique des courants dans le vide étant de déterminer les forces qui s’exercent entre ces courants, les deux lois précédentes suffisent pour exprimer ces forces, et, en principe, on peut considérer que toutes les actions magnétostatiques peuvent être comprises à partir de la loi de Biot et Savart et de la loi de Laplace. En fait, pour des circuits de formes quelconques, les calculs seraient longs ; aussi est-il avantageux d’arriver plus simplement au résultat ou à certaines conclusions en utilisant quelques propriétés caractéristiques du vecteur induction et quelques méthodes générales de tracé de champ.

Propriétés du vecteur induction magnétique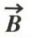

Ces propriétés se déduisent de la loi de Biot et Savart au moyen de transformations mathématiques ; il leur correspond un sens physique bien précis.

• Première propriété. Le vecteur induction magnétique satisfait en chaque point à la condition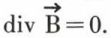

Cette propriété mathématique signifie que le vecteur est à flux conservatif ou encore que le flux de à travers une surface fermée quelconque est nul, cette surface coupant ou non les courants.

Pour qu’il en soit ainsi, les lignes de force du vecteur induction s’enroulent autour des conducteurs ; un tel champ de vecteurs est dit solénoïdal.

• Seconde propriété. Le vecteur induction magnétique dérive d’un potentiel-vecteur .

Cela signifie qu’on peut trouver un champ de vecteurs satisfaisant à la condition Cette propriété découle du fait mathématique que est toujours égal à zéro. Il est à noter, cependant, que le potentiel-vecteur n’est ainsi défini qu’à un gradiant près, celui d’un potentiel scalaire, puis est aussi toujours égal à zéro.

On peut arbitrairement remplacer le potentiel-vecteur par 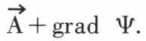Cette transformation est dite transformation de jauge. On conçoit, du reste, qu’une telle transformation est possible, puisque, pour qu’un champ de vecteurs soit complètement défini, il est nécessaire de connaître à la fois son rotationnel et sa divergence ; or, le rotationnel est seul imposé ; par suite, nous pouvons donner à la forme que nous souhaitons.

En magnétostatique, on utilise généralement la jauge de Coulomb

Pour un circuit filiforme, l’expression du potentiel-vecteur satisfaisant à cette condition est

et, pour une répartition en volume de la densité de courant, elle est

Le potentiel-vecteur est défini même en un point sur les courants. L’expression du potentiel-vecteur a la même forme que celle du potentiel scalaire électrique pour une répartition de charges en volume ; le potentiel-vecteur a en magnétostatique le rôle du potentiel scalaire en électrostatique ; c’est un intermédiaire pour déterminer le champ.

Considérons l’exemple d’une ligne à courant continu avec deux conducteurs, C₁ et C₂, très longs et parallèles à Oz (fig. 4). Les propriétés magnétiques dans tout l’espace se déduisent de celles dans un plan P, perpendiculaire à Oz, par translation parallèle à Oz. Le potentiel-vecteur en un point M à la distance r₁ de C₁ et r₂ de C₂ ne possède que la composante A_z, qui a pour amplitude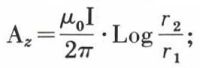

il en résulte que le vecteur induction est dans le plan xOy ; on montre alors que l’équation des lignes de force de est A_z = C^te ; ces lignes de force forment dans le plan un faisceau de circonférences dont les points de base sont les intersections des conducteurs C₁ et C₂ avec le plan P ; elles coïncident avec les équipotentielles du champ électrique.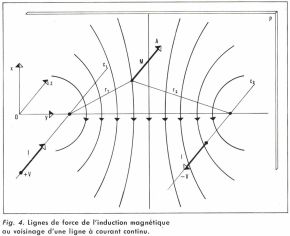

Le théorème d’Ampère et le champ magnétique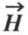

Considérons un circuit C dans le vide (fig. 5), parcouru par l’intensité I ; il crée en chaque point de l’espace l’induction . On montre alors que la circulation de le long d’une courbe Γ, entre deux points M₁ et M₂, est donnée par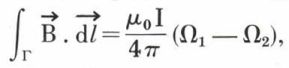

Ω étant l’angle solide sous lequel on voit le circuit C du point M. C’est la relation intégrale exprimant le théorème d’Ampère dans le vide.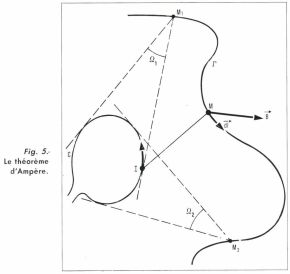

Si Γ est une courbe fermée, deux cas se présentent.
1. Γ n’enlace pas le circuit C :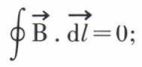

tout se passe comme si dérivait d’un potentiel scalaire

corrélativement, puisque est toujours égal à zéro ; il est à noter que cette dernière expression n’est valable qu’en dehors des courants.
2. Γ enlace une fois le circuit C ;

ne dérive plus d’un potentiel scalaire ; et si la répartition de courant est en volume, avec la densité , cette relation intégrale peut être transformée en une relation différentielle

Il est important de retenir que cette dernière expression concerne des courants dans le vide ; elle s’écrit différemment dans un milieu matériel. C’est du reste pour établir une relation valable dans tous les cas qu’on est amené à définir dans le vide le vecteur champ magnétique 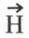comme le rapport et qu’on écrit le théorème d’Ampère sous la forme générale

Le théorème d’Ampère est d’une utilisation très pratique pour le calcul de l’induction créée par des circuits présentant une symétrie, notamment la symétrie cylindrique ; on peut, en général, calculer simplement la circulation de l’induction magnétique le long d’une ligne de force. Par exemple, on établit de cette manière que l’induction sur l’axe d’un solénoïde de longueur l, à l’intérieur de celui-ci, est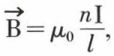

le solénoïde comprenant n spires parcourues par l’intensité I. L’induction au centre d’un solénoïde de 1 m de longueur et constitué de 500 spires parcourues par un courant de 5 A est de 3,14.10^–3 T, ou 31,4 Œ.