logiques modales (suite)

Afin de tenter de remédier à cet état de choses, il est possible de renoncer à l’idée que la valeur de vérité d’une proposition composée est seulement fonction des valeurs de vérité de ses composantes (point de vue de l’extension), et d’introduire un lien plus exigeant en posant : p ≺ q = df ~ ⃟ (p ⋀ ~ q). On ne relie p à q par un lien d’implication que s’il est impossible d’avoir simultanément p vraie et q fausse.

On peut alors construire un système de l’implication stricte en prenant pour seuls symboles primitifs les variables de propositions, les opérateurs unaires ~ et ⃟ et l’opérateur binaire ⋀. On construit l’ensemble des ebf. On pose enfin les définitions usuelles pour ⋁, ⊃ et ≡, et de plus :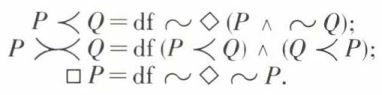

Axiomes

as1 (p ⋀ q) ≺ (q ⋀ p) ;

as2 (p ⋀ q) ≺ p ;

as3 p ≺ (p ⋀ p) ;

as4 (p ⋀ (q ⋀ r)) ≺ (p ⋀ (q ⋀ r)) ;

as5 ((p ≺ q) ≺ (q ≺ r)) ≺ (p ≺ r) ;

as6 (p ⋀ (p ≺ q)) ≺ q.

En introduisant des règles de substitution convenables (substitution d’ebf aux variables de proposition et substitution d’équivalences strictes), une règle qui dit que si P et Q sont des théorèmes, alors P ⋀  ⋀ Q en est un et la règle du détachement pour ≺, c’est-à-dire : si P et P ≺ Q sont des théorèmes, Q est un théorème, on a construit un système connu sous le nom de s1.

Si les expressions p ≺ (q ≺ p) et ~ p ≺ (p ≺ q) ne sont pas des théorèmes de s1, en revanche on a :
⊢ □ p ⊃ (q ≺ p) et ⊢ ~ ⃟ p ⊃ (p ≺ q),
qui conservent un aspect paradoxal. Il est vrai qu’il ne concerne pas uniquement l’implication stricte, puisque les formules contiennent le signe ⊃.

En tant que système modal, s1 est contenu en t, c’est-à-dire que tous les théorèmes de s1 sont des théorèmes de t, mais pas inversement. On a, en particulier, le théorème ⊢ (p ≺ q) = □ (p ⊃ q) qui justifie l’usage d’un même signe pour la conditionnelle stricte en s1 et en t.

Si l’on rajoute à s1 l’axiome suivant :
as6 ⃟ (p ⋀ q) ≺ ⃟ p,
on obtient le système dit « s2 ». Il est caractérisé par l’existence d’une règle (la règle de Becker) qui dit que, si P ≺ Q est un théorème, alors □ P ≺ □ Q en est un. Mais, du point de vue des paradoxes, il contient les théorèmes :
⊢ □ p ≺ (q ≺ p) et ⊢ ~ ⃟ p ≺ (p ≺ q),
ou paradoxes de l’implication stricte, plus gênants encore, s’il y a gêne, que ceux de s1.

s2 est aussi contenu dans t.

Les systèmes modaux s1, s2 comme t ne contiennent pas de théorèmes qui permettent de réduire le nombre des modalités. Ajoutons donc encore l’axiome suivant :
as7 (p ≺ q) ≺ (~ ⃟ q ≺ ~ ⃟ p).

Il suffit à obtenir le système s3, qui ne contient alors que 42 modalités (40 modalités propres et les 2 modalités impropres). Ainsi construit, s3 contient manifestement s2, mais on montre que s3 n’est plus contenu en t.

L’approche des modalités à travers la recherche d’une implication stricte diffère un peu de celle qui a servi de point de départ à t. En particulier, la nécessité n’y a pas exactement la même signification, en ce sens que la règle N, qui exprimait la condition (4), n’y est universellement valide. Ainsi, dans s1 par exemple, on a seulement que, si P est un théorème du calcul classique des propositions, donc une expression sans □ ni ⃟, alors □ P est un théorème de s1. Nous sommes donc en présence d’une interprétation de la nécessité plus restrictive qu’en t.

Il est cependant possible de retrouver s4 à partir de s3 en ajoutant l’axiome suivant (qu’il suffirait d’ailleurs d’ajouter à s1) : as8 ⃟ p ≺ ⃟⃟ p.

En résumé, on a la situation représentée par le schéma (fig. 2) dans lequel X → Y signifie que le système X contient le système Y.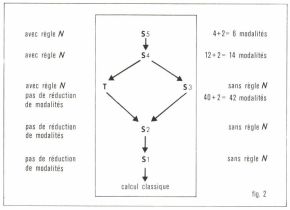

Notons encore que tous ces systèmes peuvent être présentés de multiples façons et qu’ils ne constituent qu’un petit nombre de ceux qui ont été étudiés.

On a construit des systèmes analogues aux s_i, systèmes qui ne contiennent pas le théorème □ p ⊃ p ; des systèmes dont aucun théorème n’a la forme □P ; des systèmes qui reposent sur la logique intuitionniste (v. calcul des propositions), etc.

Logiques modales des prédicats

De même que les systèmes précédents prenaient pour base le calcul des propositions, de même il est possible de construire des logiques modales qui partent du calcul des prédicats. On se heurte toutefois à certaines difficultés qui reposent sur le parallélisme que nous avons noté entre les opérateurs ∀ et ∃ d’une part et □ et ⃟ de l’autre. En particulier, si l’on ajoute les axiomes modaux de t (a4 et a5) à un système d’axiomes de la logique des prédicats, on peut facilement prouver le théorème ⊢ □ (∀ x) ax ⊃ (∀ x) □ ax, mais pas la réciproque, pourtant assez intuitive et connue sous le nom de formule de Barcan.

Logiques déontiques

Dans la mesure où l’on peut considérer les systèmes t et s_i comme des systèmes formels, il est possible d’en chercher d’autres interprétations. En particulier, on peut tenter d’interpréter
□ p comme p est obligatoire ;
⃟ p comme p est permise.
Il est cependant évident qu’aucun des systèmes précédents n’autorise une telle façon de voir. Tous, en effet, contiennent les deux théorèmes :
⊢ □ p ⊃ p et ⊢ p ⊃ ⃟ p,
qui signifieraient alors respectivement : « Si p est obligatoire, p est le cas » et « si p est le cas, p est permise ». Ce serait là une vue bien optimiste de la nature humaine ! En revanche, il semble convenable d’accepter le théorème ⊢ □ p ⊃ ⃟ p, soit « ce qui est obligatoire est permis ». On pourrait donc songer à modifier les systèmes aléthiques pour supprimer les deux premiers théorèmes, tout en conservant le troisième.

On n’a là qu’une façon d’aborder la question, et la logique déontique a fait l’objet de nombreuses autres approches.

J.-B. G.

 G. H. von Wright, An Essay in Modal Logic (La Haye, 1951). / C. I. Lewis et C. H. Langford, Symbole Logic (New York, 1959). / R. Feys, Modal Logic (Nauwelaerts, Louvain et Gauthier-Villars, 1965). / G. E. Hughes et M. J. Cresswell, An Introduction to Modal Logics (Londres, 1968). / G. Kalinowski, la Logique des normes (P. U. F., 1972).