anneau (suite)

Idéal dans un anneau

Un idéal bilatère d’un anneau A est un sous-groupe additif de A multiplicativement permis. Il vérifie les conditions suivantes :
a) si a ∈  et b ∈ , a – b ∈  ;
b) a ∈  entraîne ax ∈  et xa ∈ , pour tout x de A.

La première condition est nécessaire et suffisante pour que soit un sous-groupe additif de A. La seconde traduit le fait que est multiplicativement permis à droite et à gauche, donc multiplicativement permis. En se restreignant à l’une des deux conditions (a ∈  ⇒ ax ∈ ) ou (a ∈  ⇒ xa ∈ ), on obtient les notions d’idéal à droite ou d’idéal à gauche. Dans un anneau commutatif, ces deux notions se confondent avec celle d’idéal bilatère ou, simplement, d’idéal.

• Dans l’anneau ℤ des entiers relatifs, le sous-ensemble des nombres pairs est un idéal, car la différence de deux nombres pairs est un nombre pair et le produit d’un nombre pair par un nombre quelconque est aussi un nombre pair.

• Plus petit idéal à gauche contenant un élément a de A. Cet idéal doit contenir a + a = 2a, 3a, etc., puis a – a = 0, – a, – 2a, etc. ; donc tout élément de la forme na, où n est un entier relatif, puis tout élément de la forme xa, où x est un élément quelconque de a ; donc tout élément de la forme na + xa, quels que soient n ∈ ℤ et x ∈ A.

Mais l’ensemble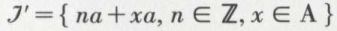

vérifie les deux conditions intervenant dans la définition d’un idéal. Donc est l’idéal cherché. C’est l’idéal à gauche engendré par a ; on peut le noter (a} ; il est principal, car engendré par un seul élément.

Cet exemple donne un moyen simple de construire des idéaux dans un anneau. Si l’anneau A possède un élément-unité e, l’élément na s’écrit
na = n.ea = ne.a = sa
avec s = ne ∈ A : d’où
na + xa = sa + xa = ta
avec t = s + x ∈ A.

Par suite, l’idéal principal à gauche engendré par a coïncide avec l’ensemble des éléments de la forme ta, où t décrit A ; on écrit alors (a} = Aa.

On développe des considérations analogues avec l’idéal à droite engendré par un élément de l’anneau.

• Idéal bilatère principal (a). C’est l’idéal bilatère engendré par a ou plus petit idéal bilatère contenant a. Si l’anneau est commutatif, (a) = {na + xa, n ∈ ℤ, x ∈ A}. Si, en outre, l’anneau est unitaire, na = ne.a et ne ∈ A ; les produits na et xa ont même forme ; par suite, a = Aa = aA, ensemble des multiples de a. Mais si l’anneau possède un élément-unité sans être commutatif,
(a) = {x₁ax₂, x₁ ∈ A, x₂ ∈ A} = AaA.

• L’anneau ℤ des entiers relatifs, commutatif et unitaire, fournit un champ d’application à ces considérations. Par exemple, (2) et (5) sont deux idéaux de ℤ respectivement formés des multiples de 2 et de 5. Les nombres 4 et 7 engendrent l’idéal (4, 7) = {4λ + 7μ, λ ∈ ℤ, μ ∈ ℤ} ;
29 ∈ (4, 7),
car 29 = 8 + 21 = 4 × 2 + 7 × 3.

Les idéaux (12, 18), (30, 42) et (6) sont égaux ; on vérifie, en effet, que 30 = 5 × 6 et que 42 = 7 × 6, donc (30) ∈ (6) et (42) ∈ (6) ; d’où (30, 42) ⊂ (6) [⊂, signe de l’inclusion] ; mais
6 = 30 . 3 – 42 . 2 ;
donc 6 ∈ (30, 42) et (6) ⊂ (30, 42) ; d’où (6) = (30, 42). De même, 18 = 3 × 6 et 12 = 2 × 6 ; d’où (12, 18) ⊂ (6) ; mais 6 = 18 – 12 ; d’où (6) ⊂ (12, 18), et (6) = (12, 18). On démontre que dans ℤ tout idéal est principal, c’est-à-dire engendré par un seul élément.

• S’il est possible d’engendrer des idéaux à l’aide d’éléments d’un anneau, il est aussi possible d’obtenir de nouveaux idéaux à partir d’idéaux déjà connus.

— Soit deux idéaux à gauche, et d’un anneau A et

Cet ensemble est un sous-groupe additif de A. De plus, pour tout élément s de A,
sa = sx₁ + sx₂ = x′₁ + x′₂,
avec et . Donc sa appartient à , qui est ainsi multiplicativement permis à gauche et qui, par suite, est un idéal à gauche. C’est le plus petit idéal à gauche contenant et  ; on le note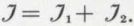

On peut généraliser à une somme de plus de deux idéaux. Ainsi, dans ℤ, où tout idéal est principal, l’idéal (a) + (b) est un idéal (d), d étant le P. G. C. D. de a et de b. Ce résultat, aisément établi à l’aide de la théorie des idéaux dans ℤ, fournit un vocabulaire : l’idéal-somme de deux idéaux est appelé le plus grand commun diviseur de ces deux idéaux. On généralise à plus de deux idéaux.

• L’intersection de deux idéaux , et (ensemble des éléments communs à et ) est aussi un idéal, à gauche, ou à droite, ou bilatère, en même temps que et . Dans ℤ, l’intersection des deux idéaux (a) et (b) est l’idéal (m), où m est le P. P. C. M. de a et de b. Ce résultat est à l’origine d’une dénomination : de façon générale, l’intersection de deux idéaux est appelée le plus petit commun multiple de ces deux idéaux. On généralise à plus de deux idéaux.

Idéaux et relations d’équivalence

Dans un anneau A, tout l’idéal à gauche définit une relation d’équivalence sur les éléments de A compatible à gauche avec la multiplication de A. Cette relation notée ℝ se traduit par xℝy si et seulement si x – y ∈ , x ∈ A et y ∈ A.

On vérifie qu’elle est réflexive, car x – x = 0 ∈  ; symétrique, car si x – y ∈ , y – x = – (x – y) ∈  ; transitive, car si x – y ∈  et

x – z = (x – y) + (y – z) ∈  ; c’est une relation d’équivalence. De plus, xℝy entraîne axℝay, quel que soit l’élément a de A, car x – y ∈  entraîne a(x – y) ∈  ou ax – ay ∈ , ce qui traduit la compatibilité à gauche de la relation avec la multiplication. Les classes d’équivalence sont les complexes , qui sont distincts. On définit une notion semblable avec un idéal à droite. Enfin, il y a correspondance biunivoque entre les relations d’équivalence compatibles (à droite et à gauche) avec la multiplication de l’anneau et les idéaux bilatères de l’anneau ; par exemple dans ℤ, la relation x – y ∈ (5) ; l’ensemble quotient est l’ensemble ℤ/5 = {0, 1, 2, 3, 4} des classes résiduelles modulo 5 ; c’est un corps commutatif.