analyse (suite)

Les calculs approchés babyloniens et grecs

À un très humble degré, l’analyse apparaît donc dès qu’apparaissent des procédés illimités de calcul. Sans que l’on puisse affirmer avec certitude que de tels algorithmes se trouvent dans la mathématique babylonienne, on doit noter cette valeur approchée de qui figure dans une tablette de la Haute Époque : 1 ; 24, 51, 10 (numération sexagésimale de position). Plus nettement, le procédé de Héron d’Alexandrie (i^er s. apr. J.-C.) pour extraire une racine carrée est nettement conçu comme illimité : soit A le nombre dont on veut calculer la racine. On part d’une approximation arbitraire a₀ et l’on calcule

On recommence à partir de a₁ et l’on continue aussi loin qu’on le désire. De tels procédés, ou d’autres analogues, se retrouvent chez tous les calculateurs du Moyen Âge et de la Renaissance. Il convient toutefois de signaler la règle des nombres moyens formulée en 1484 par Nicolas Chuquet (v. 1445-v. 1500) : Pour résoudre toute équation f(x) = 0 (notations actuelles), on prend deux fractions et telles que

et l’on forme la quantité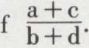

On recommence indéfiniment les calculs en prenant pour nouvelles bornes une des précédentes et la nouvelle fraction intercalaire.

Les quantités irrationnelles

Cependant, pour que de tels algorithmes illimités soient utilisés, il fallait que les mathématiciens aient pris conscience de l’insuffisance du corps ℚ des nombres rationnels pour résoudre les problèmes essentiels de la géométrie. Car il ne peut s’agir au début que de cela, la géométrie, « science du continu », étant opposée à l’arithmétique, « science de la grandeur discrète ». C’est Aristote (384-322 av. J.-C.) qui nous rapporte la première preuve, due aux pythagoriciens, de l’existence de grandeurs irrationnelles. Si l’on suppose que la quantité est rationnelle, on peut écrire les nombres p et q étant premiers entre eux. On a la relation p² = 2q² et p est pair, égal à 2r. Ainsi 4r² = 2q² ou q² = 2r², et q est pair lui aussi, ce qui est absurde. Une fois reconnue l’existence d’irrationnelles se trouvait soulevée la question épineuse : qu’est-ce que le rapport de deux grandeurs ? La réponse est donnée d’une façon magistrale au livre V des Éléments d’Euclide (iii^e s. av. J.-C.), que beaucoup, sans preuves convaincantes, veulent attribuer à Eudoxe (v. 406 - v. 355 av. J.-C.). À tout couple de grandeurs de même espèce se trouve désormais rattaché un « rapport », nous dirions un nombre réel. Ce rapport est défini par une « coupure » sur l’ensemble ℚ⁺ des nombres rationnels positifs, suivant la terminologie de Richard Dedekind (1831-1916) [Stetigkeit und irrationale Zahlen, 1872], l’auteur allemand ne faisant qu’analyser le livre V, sans le trahir. Cependant, le problème réciproque — « à toute coupure sur l’ensemble ℚ, peut-on associer le rapport de deux grandeurs ? » — ne fut jamais résolu par les Grecs ni leurs successeurs. La réponse affirmative que donne Dedekind est une des premières apparitions de l’arithmétisation de l’analyse. C’est un postulat qui définit le corps ℝ des nombres réels logiquement à partir de l’ensemble ℚ des nombres rationnels, et qui fait ainsi disparaître l’antinomie entre arithmétique et géométrie. La construction du corps ℝ des nombres réels se fait de nos jours de bien des façons, mais 1872 reste une date importante, quoique Dedekind ait eu des précurseurs comme Charles Méray (1835-1911) en France, en 1869.

Les tangentes chez les Grecs

Pour les Grecs, une courbe sépare le plan en deux domaines distincts, l’extérieur et l’intérieur, ou figure. L’extérieur peut contenir des droites illimitées dans les deux sens, ce qui n’est généralement pas le cas pour la figure. Une droite qui passe d’une des deux régions dans l’autre est une sécante. Une droite qui a un point commun avec la courbe, mais ne pénètre pas dans la figure, est dite tangente. C’est le sens du mot chez les trois grands géomètres Euclide, Archimède (v. 287-212 av. J.-C.) et Apollonios de Perga (v. 262 - v. 180 av. J.-C.), qui établissent avec une grande rigueur les propriétés des tangentes. La région comprise entre la tangente et la courbe est appelée angle de contingence. Plus petit que tout angle rectiligne sans cependant être nul, un tel être mathématique, dont l’existence contredit le livre V des Éléments, pourtant très solidement construit, amènera au Moyen Âge et à la Renaissance bien des controverses passionnées.

Diorismes

Étroitement liés au problème des tangentes sont les diorismes, ou limitations des problèmes géométriques. Le cas le plus simple se trouve au livre VI des Éléments. Il concerne la discussion de la parabole en ellipse, c’est-à-dire de l’équation du second degré. Toute équation du second degré n’a pas forcément deux racines, le cas limite étant celui où le discriminant est nul. Archimède étudie lui aussi les cas limites des problèmes solides (ici du 3^e degré) au second livre de Sur la sphère et le cylindre. Étudiant le nombre des normales menées à une conique, Apollonios trouve pour sa part les développées de ces courbes. Sir Isaac Newton (1642-1727) et Christiaan Huygens (1629-1695) seront en ce domaine ses successeurs immédiats. D’une façon générale, lorsque les problèmes solides (de degré 3 ou 4) seront résolus par intersection de deux coniques, les cas limites seront ceux où les deux courbes seront tangentes.

Géométrie de la mesure quadrature du cercle

L’étude des tangentes, de l’angle de contingence, des diorismes est à l’origine du calcul différentiel. Le calcul intégral trouve au contraire sa source dans la mesure des aires et des volumes. Le plus ancien problème qui soit ici à signaler est celui de la quadrature du cercle. Le papyrus Rhind (v. 1800 av. J.-C.) montre que, pour les Égyptiens, le diamètre d’un cercle équivalent à un carré surpasse son côté de , ce qui, pour des calculateurs qui n’utilisent que des entiers et des quantièmes, est une excellente approximation. Si les Babyloniens adoptent généralement pour le nombre π la valeur entière 3, ils utilisent aussi une meilleure approximation en prenant pour la valeur 57,36 (numération sexagésimale). Cela revient à écrire Cette approximation se retrouve dans les Sulvasūtras hindoues (entre 400 et 200 av. J.-C.), et elle est encore employée parfois en Occident au xv^e et au xvi^e s. Repris par les Grecs, le problème de la quadrature du cercle est enfin traité scientifiquement par Eudoxe et surtout par Archimède, qui établit la double inégalité