graphes (théorie des) (suite)

Petit vocabulaire du graphe orienté

arc, flèche joignant deux éléments d’un graphe distincts ou confondus. [Sur la figure a, (1,2) est un arc comme (3,4) ou (6,6). En revanche, (1,6) n’est pas un arc.]

chemin, suite d’arcs telle que l’extrémité terminale de chaque arc coïncide avec l’extrémité initiale du suivant. [On peut le noter par une suite de sommets allant de l’origine du premier arc à l’extrémité du dernier. Par exemple, sur la figure a, (2,3,4,1,5,4,3) est un chemin. On peut aussi noter un chemin par les noms des arcs qui le constituent, si l’on place une lettre sur chacun des arcs du graphe pour les désigner.]

chemin élémentaire, chemin ne passant pas deux fois par le même sommet.

chemin simple, chemin ne contenant qu’une fois un même arc. [Le chemin (1,2,3,4) est un chemin simple, alors que le chemin (1,2,3,4,3,4) n’est pas simple. Un chemin élémentaire est simple. La réciproque est fausse.]

circuit, chemin fini dont le sommet terminal coïncide avec le sommet initial.

circuit élémentaire, circuit ne passant pas deux fois par le même sommet.

circuit simple, circuit ne contenant qu’une fois un même arc.

ensemble fortement connexe maximal, graphe partiel connexe maximal contenant un élément donné. (Sur la figure b on ne peut aller du sommet 5 au sommet 1. Mais on peut, étant donné un sommet, chercher un sous-ensemble de sommets contenant le sommet choisi et formant avec lui un sous-graphe fortement connexe maximal. On trouve ainsi cinq sous-graphes fortement connexes maximaux : ce sont les sous-graphes {1,2,3}, {4,5,6}, {7,8}, {9}, et {10}. Si, en cherchant le sous-graphe connexe maximal contenant le sommet α, on trouve que le sommet β appartient à ce sous-graphe, il est inutile de reprendre la même recherche pour β : α et β appartiennent au même sous-graphe. D’ailleurs, la relation entre les sommets d’un graphe « appartenir au même sous-graphe connexe maximal » est une relation d’équivalence car elle est réflexive, symétrique et transitive.)

fermeture transitive d’un sommet x, ensemble des sommets que l’on peut atteindre en partant de x. [Notation : .]

fermeture transitive inverse d’un sommet x, ensemble des sommets d’où l’on peut atteindre x.
[Notation : . Les fermetures et se déterminent de proche en proche par un nombre d’opérations qui est nécessairement fini. L’ensemble fortement connexe maximal contenant un sommet x donné est

graphe antisymétrique, graphe ne comportant pas l’arc (y, x) s’il contient l’arc (x, y) [fig. c].

graphe fortement connexe, graphe tel qu’il existe au moins un chemin qui permet de passer de tout sommet à tout autre (fig. d).

graphe orienté, ensemble E dont les éléments sont représentés par des points et par des flèches qui indiquent une relation dans cet ensemble (fig. a).

graphe partiel, graphe obtenu en supprimant dans un graphe donné un certain nombre d’arcs tout en conservant tous les sommets.

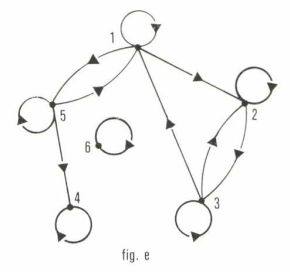
graphe réflexif, graphe dans lequel, quel que soit l’élément x d’un ensemble E, l’arc (x, x) appartient au graphe (fig. e).

graphe symétrique, graphe comportant l’arc (y, x) dès qu’il comporte l’arc (x, y) [fig. f].

graphe transitif, graphe contenant l’arc (x, z) s’il contient les arcs (x, y) et (y, z). [Dès qu’un contour triangulaire comporte deux arcs dans le même sens, il doit comporter le troisième arc, qui permet de passer du premier au troisième sommet (fig. g).]

longueur d’un chemin, nombre d’arcs qu’il contient. [Un chemin de longueur nulle contient zéro arc : il est formé par un sommet.]

partition d’un graphe en classes d’équivalence pour la relation « appartenir au même sous-ensemble fortement connexe maximal », décomposition d’un graphe en sous-graphes fortement connexes maximaux, chaque sous-graphe étant une classe d’équivalence.

[La classe d’équivalence C(x) d’un sommet x est constituée par l’ensemble des sommets que l’on peut atteindre à partir de x et d’où l’on peut partir pour arriver en x :

sommet, élément de l’ensemble E qui appartient au graphe.

sous-graphe, graphe obtenu en supprimant dans un graphe donné un certain nombre de sommets ainsi que les arcs qui en partent ou qui y aboutissent.

Petit vocabulaire du graphe non orienté

arbre, tout graphe connexe sans cycle. (C’est probablement en 1847 que Gustav Kirchhoff [1824-1887] développa, le premier, la théorie des arbres en étudiant certains circuits électriques et en cherchant les intensités des courants les parcourant. Vers 1857, Arthur Cayley [1821-1895] rencontra les arbres en chimie organique. Enfin Camille Jordan [1838-1922] développa, en 1869, cette théorie de façon désintéressée, sans se douter de la contribution qu’il apportait à la chimie organique.)

chaîne ou chemin, succession de points et de lignes.

chemin élémentaire, chemin qui n’utilise pas deux fois le même point.

chemin simple, chemin qui n’utilise pas deux fois la même ligne. (Si un chemin est élémentaire, il est simple. La réciproque n’est pas vraie : un chemin simple peut ne pas être élémentaire.)

composante connexe, sous-graphe connexe maximal d’un graphe non connexe.

cycle, chemin ou chaîne fermés.

cycle simple, cycle dont chacune des lignes qui le constituent ne figure qu’une fois.

degré d’un sommet, nombre de lignes ayant ce sommet comme lune de leurs extrémités.

diamètre d’un graphe, la plus grande distance que l’on peut trouver sur ce graphe.

distance de deux sommets, longueur du plus court chemin entre ces deux sommets.

écartement d’un sommet, la plus grande distance que l’on peut trouver à partir de ce sommet.

eulérien, se dit d’un chemin ou d’un cycle n’utilisant pas deux fois la même ligne et qui permet de décrire tout le graphe sans lever la plume, celle-ci pouvant passer plusieurs fois par certains sommets. (Cette définition s’étend à un multigraphe. Pour qu’un graphe connexe soit eulérien, il faut et il suffit que tout sommet de ce graphe soit de degré pair.)

graphe, ensemble de points et de lignes dont chacune joint deux points distincts (fig. h).

graphe complet d’ordre p, graphe dont tous les sommets sont reliés deux à deux par une ligne (fig. i). [Ce graphe est donc régulier et de degré p – 1.]

graphe connexe, graphe dans lequel il existe au moins un chemin entre deux quelconques de ses sommets.