forme linéaire (suite)
Formes linéaires d’un espace vectoriel En de dimension n
On peut d’abord remarquer que, K pouvant être assimilé à un espace vectoriel de dimension 1 sur lui-même, la dimension de l’espace image de En par une forme linéaire f ne peut être que 0 ou 1. Par suite, ou bien tout vecteur u de l’espace vectoriel En a pour image 0 dans K, ou bien le noyau de f est de dimension n – 1.
Quel que soit le cas, soit
u = x1e1 + x2e2 + ... + xnen
l’expression analytique d’un vecteur u de En dans une base (e1, e2, ..., en) de En. Comme la forme f est linéaire,
f(u) = f(x1e1 + ... + xnen) = x1f(e1) + ... + xnf(en),
toutes les formes f(ei) sont des scalaires de K d’après la définition de la forme f ; en posant
f(ei) = ai ∈ K,
l’application f est donc celle qui au vecteur u de En fait correspondre le vecteur
f(u) = a1x1 + ... + anxn.
Inversement, l’application f qui associe au vecteur u de En le scalaire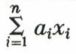 
de K, les quantités ai étant des scalaires quelconques de K, est linéaire ; de plus, f(ei) = ai puisque, pour ei, xi = 1, et xj = 0 pour j ≠ i. Ainsi une forme linéaire est complètement déterminée par la donnée des ai.
Base duale de l’espace des formes
Dans l’espace E′ des formes linéaires de En sur K, il existe n formes particulières fi, i = 1, 2, ..., n telles que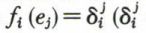 
est le symbole de Kronecker, 
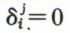si i ≠ j,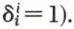 
Ces formes fi appartiennent à E′ puisque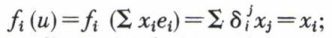 
ce sont donc des formes linéaires de E. De plus, elles sont indépendantes, car une relation de la forme λ1f1 + ... + λnfn = 0 entraîne 
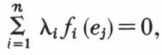quel que soit j, ce qui impose λi = 0 pour tout i puisque seul fi(ei) = 1. Enfin, toute forme f de E′ se décompose sur les formes fi ;
f = a1f1 + a2f2 + ... +anfn,
car f(u) = a1f1(u) + ... +anfn(u) ou f(u) = a1x1 + a2x2 + ... +anxn.
Les formes fi constituent donc une base de E′ qui est de dimension n. On l’appelle la base duale de la base e1, e2, ..., en de l’espace vectoriel E.
Rang d’un système de formes linéaires
Ces formes étant des vecteurs d’un espace, leur rang est la dimension du sous-espace qu’elles engendrent (résultats sur les espaces vectoriels). Ce rang est inférieur ou égal à n.
Si le nombre des formes est égal au nombre de variables, les formes du système sont dépendantes ou non suivant que le déterminant de leurs coefficients est nul ou non.
Exemples.
• Le déterminant des formes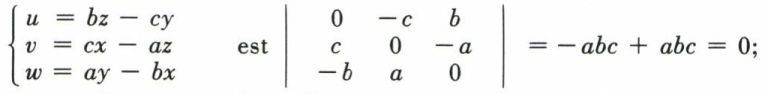
les trois formes sont dépendantes, on a au + bv + cw = 0.
• Le déterminant des formes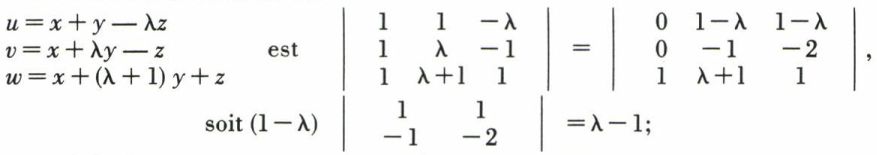
si λ ≠ 1, les formes u, v et w sont indépendantes ;
si λ = + 1, u = v, les formes sont liées.
Forme bilinéaire
On donne ce nom à toute application f de l’espace produit E × E dans le corps K de base de l’espace vectoriel E, vérifiant les propriétés suivantes :
f(u, λv1 + μv2) = λf(u, v1) + μf(u, v2)
f(λu1 + μu2, v) = λf(u1, v) + μf(u2, v),
quels que soient les vecteurs u, v, u1, u2, v1, et v2 de l’espace vectoriel E et les scalaires λ et μ de K ; ces deux relations traduisent la linéarité de l’application f par rapport à l’un des vecteurs, u ou v, quand l’autre est fixé : d’où la bilinéarité. Si E est un espace vectoriel En de dimension n, on peut exprimer deux vecteurs u et v dans une base e1, ..., en, soit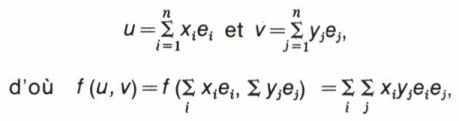
le dernier résultat étant dû à la bilinéarité de f. En posant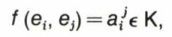
on obtient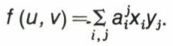 
Les scalaires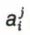 
sont au nombre de n2 ; on les range en un tableau carré qui s’appelle une matrice :
Si X et Y sont respectivement les matrices colonnes
on voit, en utilisant le produit des matrices, que
f(u, v) = XtAY,
Xt désignant la matrice transposée de X, c’est-à-dire la matrice ligne (x1, x2, ..., xn).
On a aussi f(u, v) = YtAtX, At, transposée de A, se déduisant de A par échange des lignes et des colonnes.
Rang, discriminant d’une forme bilinéaire
Le rang d’une forme bilinéaire est le rang de la matrice associée. Il est invariant dans un changement de base défini par X = PX′, Y = PY′, P étant une matrice régulière (son déterminant n’est pas nul), car
f(u, v) = XtAY = X′tPtAPY′ = X′tA′Y′,
et la matrice A′ = PtAP a même rang que A.
Le discriminant d’une forme bilinéaire est le déterminant de la matrice associée. Il n’est pas invariant dans un changement de base puisque
dét. A′ = dét. A (dét. P)2,
mais sa nullité ou sa non-nullité est invariante.
Forme bilinéaire symétrique
On appelle ainsi toute forme bilinéaire f tel que
f(u, v) = f(v, u)
quels que soient u et v dans E.
Pour que f soit symétrique, il faut et il suffit que la matrice associée A soit symétrique, c’est-à-dire que les coefficients de A symétriques par rapport à la diagonale principale (elle contient les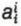 
) soient égaux : 
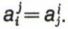Cette propriété est invariante dans un changement de base.
L’étude des formes bilinéaires symétriques conduit à celle des formes quadratiques.
E. S.
➙ Application / Déterminant / Linéaire (application) / Matrice / Quadratique.
L. Chambadal et J. L. Ovaert, Cours de mathématiques, t. I, Notions fondamentales d’algèbre et d’analyse (Gauthier-Villars, 1966). / J. Lelong-Ferrand et J.-M. Arnaudiès, Cours de mathématiques, t. I, Algèbre (Dunod, 1973). / E. Ransis, C. Deschamps et J. Odoux, Cours de mathématiques spéciales, t. I, Algèbre (Masson, 1974).