algébrique sur un anneau commutatif (équation) (suite)

b) Les coefficients a, b et c ne sont pas tous réels. On résout l’équation
az² + bz + c = 0
en complétant le carré, comme sur l’exemple suivant :
z² – 2 (2 + i)z + 7 + 4i = 0
peut s’écrire
[z – (2 + i)]² – (2 + i)² + 7 + 4i = 0
ou, après calculs,
[z – (2 + i)]² = – 4 = (± 2i)²,
car i² = – 1 ; d’où les racines
z′ = 2 + 3i et z″ = 2 – i.

Équation du troisième degré

Elle se présente sous la forme générale
az³ + bz² + cz + d = 0, a ≠ 0.
En divisant par a et en faisant le changement d’inconnue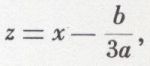

on ramène l’équation à la forme réduite

les coefficients p et q s’exprimant rationnellement en fonction de a, b, c et d.

Méthode de Cardan. On pose x = u + v, ce qui donne, en développant partiellement,
u³ + v³ + 3 uv (u + v) + p (u + v) + q = 0,
puis, en regroupant les termes en (u + v),

On cherche les solutions de l’équation (2) pour lesquelles 3uv + p = 0, c’est-à-dire qu’on résout le système

qui est équivalent au système

La deuxième équation (4) donne

u³ et v³ sont donc racines de l’équation du second degré en t :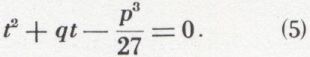

Soit α l’une des racines de l’équation (5). On pose u³ = α ; β désigne l’une des déterminations, réelle ou complexe, de

. Les trois valeurs de u possibles sont β, jβ et j ²β ; 1, j et j ² étant les racines cubiques de l’unité. La relation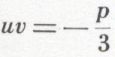

donne trois valeurs pour v :

d’où les trois racines de l’équation (1) :

Cas où p et q sont réels. Ce cas se produit, en particulier, si a, b, c et d sont réels. Le discriminant de l’équation (5) est du signe de 4 p³ + 27 q², discriminant de l’équation (1).

• Si 4 p³ + 27 q² > 0, β est réel ainsi que x₁, mais x₂ et x₃ sont imaginaires conjugués.

• Si 4 p³ + 27 q² < 0, u³ et v³, racines de l’équation (5), sont complexes imaginaires conjugués, ainsi que u et v, puisque uv est réel. Par suite, x = u + v est réel, et l’équation (1) a trois racines réelles.

• Si 4 p³ + 27 q² = 0, l’équation (5) a une racine double u³ = v³. Par suite, si u = β (réel), v = β ; si u = jβ, v = j ²β ; si u = j²β, v = jβ ; d’où x₁ = 2β et x₂ = x₃ = – β (racine double).

Pratiquement, cette méthode est peu utilisée, et lorsqu’on tente la résolution d’une équation du troisième degré, on essaie de découvrir une racine simple de cette équation (souvent entière). Ainsi, l’équation 2 z³ – z² + 3 = 0 admet la racine – 1 ; d’où la factorisation
(z + 1) (2 z² – 3 z + 3) = 0,
qui conduit aux racines – 1 et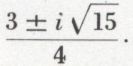

On fait aussi appel à des méthodes de calcul numérique. En voici une.

Résolution trigonométrique de l’équation du troisième degré à coefficients réels. Pour résoudre l’équation x³ + px + q = 0, on pose x = λ cos a ; d’où
λ³ cos³ a + λ p cos a + q = 0.
On identifie ensuite les deux expressions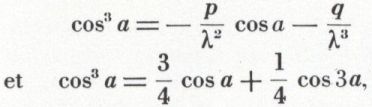

ce qui donne

Si p < 0, on obtient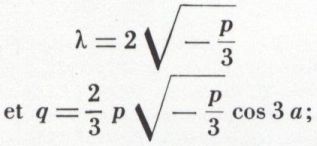

cette dernière égalité fournit cos 3 a, à condition que

ce qui est équivalent à
4 p³ + 27 q² ≤ 0.
Si on pose alors cos 3 a = cos α ou 3a = ± α + 2 k π (k = 0, 1 ou – 1), on obtient trois valeurs pour cos a et pour x :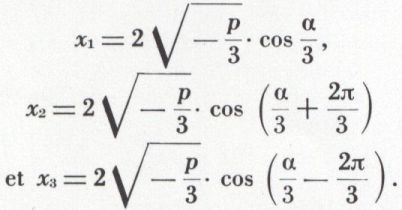

Le calcul s’achève en général à l’aide d’une table de logarithmes. Par exemple, pour
x³ – 3x + 1 = 0,
on trouve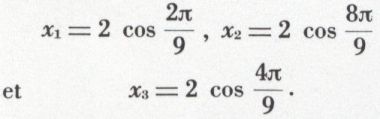

Équation du quatrième degré

Elle se présente sous la forme générale
az⁴ + bz³ + cz² + dz + e = 0, avec a ≠ 0 ;
en divisant par a, on obtient la forme
z⁴ + pz³ + qz² + rz + s = 0.

Méthode de Ferrari. Les coefficients p, q, r et s étant réels, on cherche y de façon que l’équation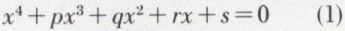

se mette sous la forme

le trinôme entre crochets étant un carré parfait. Pour cela, il suffit que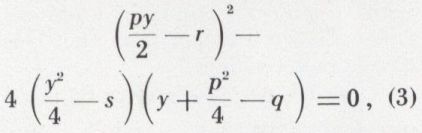

ce qui détermine y. Le premier membre de l’équation (2) est alors une différence de deux carrés et se factorise. Quant à l’équation (3), qui détermine y, elle est du troisième degré et peut, théoriquement au moins, être résolue. Par exemple, la méthode de Ferrari, appliquée à l’équation
x4 + 4 x³ – 1 = 0,
permet d’obtenir
(x² + 2 x – 1)² – 2 (x – 1)² = 0,
l’équation auxiliaire en y étant
y³ + 4y + 16 = 0,
dont une racine évidente est y = – 2.

Pratiquement, cette méthode n’est pas utilisée. Pour résoudre une équation du quatrième degré, on cherche deux racines évidentes qui ne peuvent être que des nombres assez simples, comme 1, – 1, 2, – 2, etc., et on factorise si on a pu trouver ces racines. En général, il n’en est rien et il faut faire appel à des méthodes de calcul numérique. Cependant, on sait résoudre l’équation du quatrième degré à coefficients réels dans un cas particulier : celui de l’équation bicarrée.

Exemples.
1. Pour résoudre l’équation
6 z⁴ + 5 z² – 6 = 0,
on résout l’équation

On factorise la différence de deux carrés, ce qui donne

d’où les racines

2. Pour résoudre l’équation
4 z⁴ + 3 z² + 1 = 0,
on résout l’équation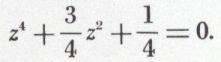

Pour cela, on regroupe

d’où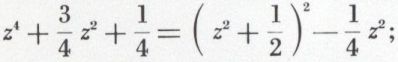

on factorise le second membre, ce qui donne

et on résout.

Équations de degré supérieur à quatre

Les équations algébriques à coefficients réels et de degré supérieur à quatre ne sont plus résolubles par radicaux. Il faut donc essayer d’abaisser leur degré soit en cherchant des racines évidentes et en factorisant, soit en faisant une transformation.

Exemple de transformation. Pour résoudre z⁵ – 1 = 0, on remarque d’abord que
z⁵ – 1 = (z – 1)(z⁴ + z³ + z² + z + 1),
ce qui fournit la racine z = 1.