cristallographie (suite)

Leonhard Sohncke (1842-1897), en ne combinant que les éléments de symétrie directe, a décrit en 1879 soixante-cinq groupes. En faisant intervenir à la fois des éléments de symétrie directe et inverse, Artur Moritz Schoenflies (1853-1928) et Ievgraf Stepanovitch Fedorov (1853-1919) ont indépendamment établi, en 1890, l’existence de deux cent trente groupes de symétrie spatiaux des milieux cristallins qui expriment le plus complètement la symétrie cristalline. La signification physique de ces théories, fondées sur la théorie des groupes de déplacement, est demeurée obscure jusqu’à la découverte de la diffraction cristalline des rayons X. Ceux-ci fournissent aisément le groupe de symétrie d’un cristal, dont la connaissance est essentielle pour déterminer sa structure atomique.

Les systèmes cristallins

Dans chacun des sept systèmes, caractérisés par la symétrie de son ou ses réseaux, se répartissent les trente-deux classes de symétrie d’orientation. À chacune d’elles, il correspond des formes cristallines caractéristiques, désignées par { h k l } et constituées par l’ensemble des faces équivalentes (mêmes propriétés géométriques, physiques et chimiques), obtenues en faisant subir à la face (h k l) les opérations de symétrie du groupe. Soit, comme exemple, la classe définie par un axe d’ordre 4 associé à un centre de symétrie, ce qui entraîne un plan de symétrie (ou miroir) perpendiculaire à l’axe. Le symbolisme international de cette classe est 4/m. Le degré de symétrie directe (axe A₄) vaut S = 4 ; le degré de symétrie inverse est toujours soit nul, soit égal au degré de symétrie directe ; le degré de symétrie totale est ici 2 S = 8. Une face inclinée sur l’axe A₄ fournit par rotation une pyramide quadrangulaire qui se répète par symétrie dans le miroir, et la forme cristalline est une dipyramide (ou octaèdre) quadratique (ou tétragonale) [fig. 8].

Système triclinique

Aucun axe de symétrie ; un seul réseau, dont la maille est un parallélépipède quelconque défini par ses trois côtés a, b, c et les trois angles α, β, γ de ces côtés ; deux classes de symétrie :

1. Holoédrie Avec un centre de symétrie 2 S = 2. Toutes les formes sont constituées par deux faces parallèles, ou pinacoïdes ;

2. Hémiédrie 1. Aucun élément de symétrie S = 1. Toutes les formes sont une seule face.

Système monoclinique

Deux réseaux de symétrie 2/m, caractérisés l’un par une maille qui est un prisme oblique à base rectangulaire (réseau P), l’autre par le même prisme, dont la base rectangulaire est centrée (réseau C) [fig. 9] ; cette maille est définie par a b c et β, angle de et l’axe binaire est généralement choisi suivant l’axe Trois groupes de symétrie ponctuelle :

1. Holoédrie 2/m. 2 S = 4. La forme générale { h k l } est un prisme ; { 010 } est un pinacoïde parallèle à m ; { h 0 l } sont des pinacoïdes.

2. Hémiédrie axiale ou énantiomorphe 2 ; degré de symétrie S = 2. La forme générale { h k l } est un dôme, ou dièdre ;

3. Antihémiédrie m. Degré de symétrie 2 S = 2. La forme générale est un dôme. Les deux hémiédries 2 et m sont compatibles avec les phénomènes de pyroélectricité et de piézo-électricité.

Système orthorhombique

La maille est un prisme droit rectangulaire défini par a b c. Elle peut être : simple, réseau P ; ou à base centrée, réseau C ; ou centrée, réseau I ; ou à faces toutes centrées, réseau F (fig. 10). Trois groupes de symétrie ponctuelle :

1. Holoédrie 2/m 2/m 2/m. 2 S = 8. La forme générale { h k l } est une dipyramide (ou octaèdre) orthorhombique ; { 0 k l }, { h 0 l }, { h k 0 } sont des prismes ; { 100 }, { 010 }, { 001 } sont des pinacoïdes ;

2. Hémiédrie holoaxe 2 2 2. S = 4. La forme générale { h k l } est un disphénoïde (ou tétraèdre) orthorhombique. Compatible avec la piézo-électricité ;

3. Antihémiédrie 2 m m. 2 S = 4. La forme générale { h k l } est une pyramide orthorhombique. Symétrie compatible avec la pyro-électricité et la piézo-électricité.

Système quadratique

L’axe A₄ est c. La maille définie par les deux paramètres a et c est un prisme droit à base carrée, réseau P ; elle peut être centrée, réseau I (fig. 11). Il comprend sept classes de symétrie :

1. Holoédrie 4/m 2/m 2/m. 2 S = 16. La forme générale { h k l }, avec seize faces, est une dipyramide ditétragonale (fig. 12) ; { h k 0 } est un prisme ditétragonal ; { 0 k l } et { h k l } sont des dipyramides tétragonales ; { 100 } et { 110 } sont des prismes tétragonaux ; { 001 } est un pinacoïde ;

2. Hémiédrie holoaxe 4 2 2. S = 8. { h k l } est un trapézoèdre tétragonal (fig. 13). Compatible avec la piézo-électricité et le pouvoir rotatoire ;

3. Antihémiédrie 4 m m. 2 S = 8. { h k l } est une pyramide ditétragonale (fig. 14). Pyro-électricité et piézo-électricité possibles ;

4. Parahémiédrie 4/m. 2 S = 8. { h k l } est une dipyramide tétragonale (fig. 8) ;

5. Hémiédrie sphénoédrique 2 S = 8. { h k l } est un scalénoèdre tétragonal (à huit faces) [fig. 15]. Piézo-électricité possible ;

6. Tétartoédrie énantiomorphe 4. S = 4. { h k l } est une pyramide tétragonale. Pyro-électricité, piézo-électricité et pouvoir rotatoire possibles ;

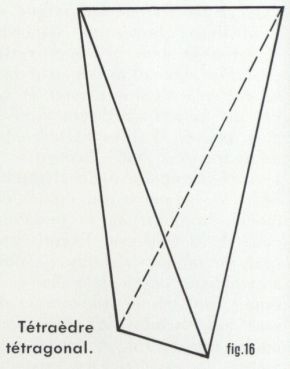
7. Tétartoédrie sphénoédrique 2 S = 4. { h k l } est un disphénoèdre tétragonal ou tétraèdre (fig. 16). Piézo-électricité possible.