cinétique (suite)
La valeur du moment d’inertie I′ d’un corps par rapport à un axe parallèle à l’axe de rotation, pour lequel le moment d’inertie est I, se calcule aisément. Si h est la distance séparant les deux axes, on a :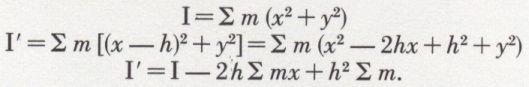
Si l’axe de rotation passe par le centre de gravité,
Σ mx = 0.
En posant M = masse totale = Σ m, on trouve
I′ = I + h2M.
Moment cinétique
La quantité de mouvement est le produit de la masse par la vitesse ; on lui attribue la même direction vectorielle qu’à la vitesse ; comme l’accélération totale γ est la dérivée géométrique de la vitesse, la force m γ est la dérivée géométrique de la quantité de mouvement m v. En projetant sur un axe, par exemple sur l’axe ox, on a la relation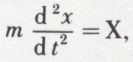
qui peut s’écrire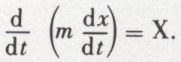
En projection sur un axe quelconque, la dérivée de la quantité de mouvement est égale à la projection de la force. En multipliant les deux membres par dt, on obtient ce qu’on appelle l’impulsion élémentaire d’une force, qui est le produit de cette force par dt :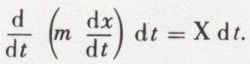
La différentielle de la quantité de mouvement projetée sur un axe est égale à l’impulsion de la projection de la force. Si l’on intègre pour un intervalle de temps quelconque, on obtient :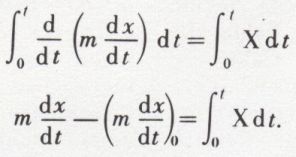
L’accroissement de la quantité de mouvement est égal en projection à la somme (ou « intégrale ») des impulsions élémentaires.
Le moment cinétique n’est autre que le moment de la quantité de mouvement. Les deux équations
conduisent à la suivante :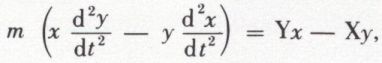
que l’on peut écrire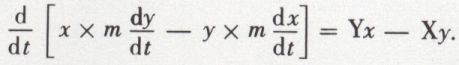
La quantité entre crochets est le moment de la quantité de mouvement par rapport à l’axe des z. Le second membre est le moment de la force par rapport au même axe. La dérivée du moment cinétique par rapport à un axe est égale au moment de la force par rapport à cet axe.
En multipliant par dt, on peut encore dire : La différentielle du moment cinétique est égale au moment de l’impulsion élémentaire.
L’intégration fournit la relation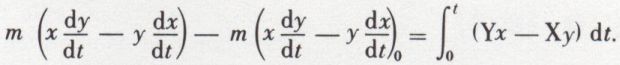
Cette relation constitue une intégrale quand le moment (Yx – Xy) de la force est une fonction connue du temps. Si, en particulier, la force rencontre constamment l’axe, le second membre est nul, et il suffit, pour obtenir une intégrale, d’écrire que le moment de la quantité de mouvement est constant. L’expression x dy – y dx mesure le double de l’aire dA balayée dans le temps dt par le rayon vecteur allant de l’origine à la projection du mobile sur le plan xoy ; 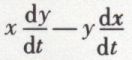 est le double de la vitesse aréolaire
est le double de la vitesse aréolaire 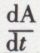 de cette projection. Le théorème du moment cinétique peut donc s’énoncer sous la forme géométrique suivante, qui constitue le théorème des aires : En projection sur un plan perpendiculaire à un axe fixe, le double produit de la masse par l’accroissement de la vitesse aréolaire est égal à l’intégrale des moments des impulsions de la force. Quand la force rencontre constamment l’axe, l’aire projetée varie proportionnellement au temps.
de cette projection. Le théorème du moment cinétique peut donc s’énoncer sous la forme géométrique suivante, qui constitue le théorème des aires : En projection sur un plan perpendiculaire à un axe fixe, le double produit de la masse par l’accroissement de la vitesse aréolaire est égal à l’intégrale des moments des impulsions de la force. Quand la force rencontre constamment l’axe, l’aire projetée varie proportionnellement au temps.

Énergie cinétique
Gottfried Wilhelm Leibniz* avait donné le nom de force vive au double de l’énergie de mouvement d’un corps, c’est-à-dire au produit de la masse par le carré de sa vitesse. Comme on a plus souvent à considérer le demi-produit 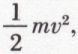 c’est à lui que Gustave Gaspard Coriolis (1792-1843) a proposé d’attribuer le nom de force vive. Celui-ci n’est pas heureux, car ce produit n’a pas les dimensions d’une force, mais celle d’un travail :
c’est à lui que Gustave Gaspard Coriolis (1792-1843) a proposé d’attribuer le nom de force vive. Celui-ci n’est pas heureux, car ce produit n’a pas les dimensions d’une force, mais celle d’un travail :
ML2T–2 = MLT–2 × L.
Pour éviter toute confusion, on continue généralement à appeler force vive le produit de la masse par le carré de la vitesse, mais on donne à la demi-force vive le nom d’énergie cinétique, qui représente d’ailleurs l’énergie de mouvement d’un corps.
La force vive a les mêmes dimensions qu’un travail ML2T–2, et il existe entre ces deux quantités une relation fondamentale. Le travail 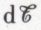 de la force F pour un déplacement dS de son point d’application est
de la force F pour un déplacement dS de son point d’application est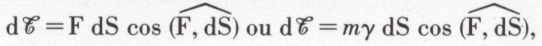
mais 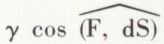 est l’accélération tangentielle
est l’accélération tangentielle 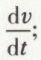 donc
donc 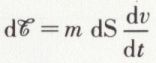 ou encore
ou encore 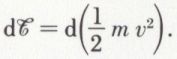
Le travail élémentaire d’une force est égal à la demi-variation de la force vive, c’est-à-dire à la variation de l’énergie cinétique.
D’une manière générale, le travail élémentaire d’une force F, de composantes X, Y et Z, est
X dx + Y dy + Z dz.
Du temps O à t, on a, en intégrant, 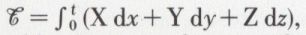 mais, pour que cette intégrale ait un sens, il faut qu’il existe une fonction de force φ ou un potentiel U (fonction de force changée de signe). Dans ce cas, on a
mais, pour que cette intégrale ait un sens, il faut qu’il existe une fonction de force φ ou un potentiel U (fonction de force changée de signe). Dans ce cas, on a
X dx + Y dy + Z dz = dφ et ∫ X dx + Y dy + Z dz = φ – φ0.
Au bout d’un temps quelconque, la demi-variation de force vive (ou variation de l’énergie cinétique) est égale à la variation de la fonction de forces. Le potentiel étant – φ, soit U = – φ, on peut écrire l’équation des forces vives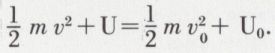
Le second membre, se rapportant à l’instant initial, est une quantité constante. Dans la suite du mouvement, l’énergie cinétique et le potentiel ont une somme constante ; l’une de ces quantités gagne à chaque instant ce que perd l’autre, comme s’il s’effectuait un échange entre elles.
Théorème des forces vives ou théorème des énergies cinétiques
Le travail de la force F pour un déplacement dS faisant un angle 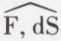 avec la direction de la force est
avec la direction de la force est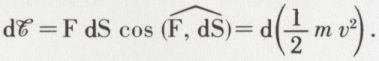
La demi-variation de la force vive, ou variation de l’énergie cinétique, est égale, à chaque instant, à la somme des travaux élémentaires de toutes les forces (forces extérieures et forces intérieures, comprenant, pour un système, les forces de liaison). Les forces intérieures au corps (et les forces de liaison dans un système) travaillent lorsque les travaux élémentaires de l’action exercée par un point A sur un point B et de la réaction de B sur A ne sont pas égaux et de signes contraires, c’est-à-dire lorsque les déplacements des deux points A et B n’ont pas même projection sur la droite AB et, par conséquent, que la distance AB varie. Il n’y a pas de travail des forces intérieures dans le cas des corps incompressibles et, au contraire, il y a travail de ces forces dans le cas des corps compressibles, notamment dans le cas des fluides gazeux.
L’énergie totale est constante et a pour valeur la somme de l’énergie cinétique (demi-force vive ou énergie de mouvement) et de l’énergie potentielle (ou énergie en puissance, comprenant l’énergie de position [altitude] et l’énergie de pression [hauteur piézométrique]).
Exemples d’application. Vitesse Vh d’un corps de masse m à l’altitude h qui, tombant sous l’influence de la pesanteur, est animé à l’altitude H d’une vitesse VH.
Le théorème des forces vives s’écrit ici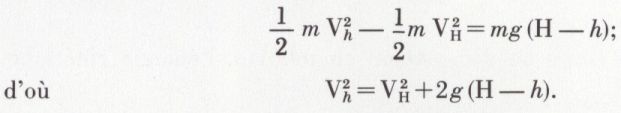
Le travail de la pesanteur (ou potentiel terrestre) est mg (H – h) entre la hauteur H et la hauteur inférieure h.
Demi-force vive ou énergie cinétique d’un corps animé d’un mouvement de rotation autour d’un axe.




