calcul numérique (suite)

Erreur absolue

La quantité inconnue x, que l’on cherche à calculer, ne pourra pas, en général, être obtenue exactement. Elle peut être la valeur théorique d’une expression compliquée indiquant des calculs qui ne conduisent qu’à une valeur numérique approchée. Elle peut être aussi la racine d’une équation connue, dont on sait qu’elle existe, mais dont on ne peut même pas donner une expression théorique ; par exemple, l’équation x⁵ – 5x + 1 = 0 a une racine comprise entre 0 et 1, car le polynôme f(x) ≡ x⁵ – 5x + 1 est décroissant dans l’intervalle [0,1], f(0) = 1 et f(1) = – 3. Mais on calculera une valeur approchée de cette racine par une méthode d’approximations successives n’utilisant nullement une expression théorique.

Ces deux exemples montrent qu’en général on obtient non pas la véritable valeur x de l’inconnue, mais une valeur voisine a, ou valeur approchée. La différence | a – x |, qui est inconnue, s’appelle l’erreur absolue. Généralement, on peut en connaître une limite supérieure, ou borne supérieure, désignée habituellement par Souvent, on se contente de la connaissance de ε pour indiquer quelle est la précision du calcul, ce qui donne un encadrement de x ; par exemple, le nombre 3,141 5 est une valeur approchée du nombre π, à ε = 5.10^–4 près, ce qui signifie que 3,141 < π < 3,142. Mais on peut, dans certains cas, apporter plus de précision et indiquer si le nombre a, adopté comme valeur de x, est inférieur ou supérieur à la valeur exacte, mais inconnue ; dans le premier cas, a est une valeur approchée par défaut du nombre x ; dans le deuxième cas, une valeur approchée par excès ; par exemple, 3,141 59 est une valeur approchée par défaut du nombre π, à moins de ε = 10^–5, et le nombre 3,141 60 est une valeur approchée par excès du même nombre π, à moins de ε = 10^–5.

Un résultat numérique doit toujours être accompagné de la limite supérieure de l’erreur commise. Cette borne supérieure peut souvent être fixée à l’avance, suivant la précision que l’on désire dans le calcul.

Calcul approché des racines d’une équation

Méthode de Newton

Sur l’intervalle (α, β), la fonction f(x), représentée graphiquement, admet une racine et une seule, x, abscisse du point M ; entre x₀ et x, il n’y a pas de racines ; f′(x) et f″(x), dérivées première et seconde de f(x), existent sur l’intervalle (α, β), et f″(x) y conserve un signe constant ; f′(x₀) ≠ 0.

Si le produit f(x₀)f″ (x₀) > 0, la valeur

est une valeur approchée de x à moins de ε′ = | x₀ – x | ; a est l’abscisse du point d’intersection de la tangente en M_o à l’arc de courbe avec l’axe des abscisses ; prendre a pour valeur approchée de x, c’est remplacer un petit arc de courbe par la tangente en un de ses points. Une limite supérieure de l’erreur ε′ est

M étant une limite supérieure de | f″(x) | sur l’intervalle (x₀, x), h un nombre supérieur à | x – x₀ | ; il faut cependant prendre garde à ne pas choisir pour M et h des nombres trop grands, car on trouverait une erreur ε trop grande et le calcul n’aurait plus de sens.

Exemple. L’équation f(x) ≡ 7x⁴ – 27x³ + 8x + 29 = 0 a une racine comprise entre 3,6 et 3,7, car f(3,6) = – 26,180 8 et f(3,7) = 2,881 7 ; comme f″(x) > 0 dans l’intervalle (3,6 ; 3,7), on effectue la correction à partir de x₀ = 3,7 et l’on trouve 3,690 9 < a < 3,691 0, cet encadrement tenant compte uniquement de l’erreur de calcul dans le calcul de

est inférieure à 0,008 7, et, par suite, 3,682 < x < 3,691.

On peut appliquer de nouveau la méthode de Newton à partir de x₁ = 3,691 ; cette réitération est appliquée de façon générale.

Méthode des parties proportionnelles

Entre les nombres a et b, la fonction f(x), représentée graphiquement, admet une racine unique, x, abscisse de M ; on remplace cette valeur par l’abscisse x₀ du point P, intersection de la corde AB et de l’axe des abscisses ; AB a pour équation ce qui, pour y = 0, donne

Souvent, on utilise simultanément la méthode de Newton et la méthode des parties proportionnelles.

Calcul approché de la somme d’une série numérique

• La somme S d’une série numérique convergente à termes positifs est la limite de la somme S_p de ses p premiers termes quand p → + ∞ ; on écrit

u_p étant le terme général de la série ; par exemple, le nombre e est donné par

On peut donc écrire S = S_p, + R_p, R_p étant le reste, inconnu, de la série. Un calcul approché de S consiste à évaluer une limite supérieure de R_p, à calculer une valeur approchée de S_p et à indiquer l’erreur commise en remplaçant S par S_p, cette erreur tenant compte de l’évaluation de R_p et de l’erreur de calcul sur S_p.
1. Si la série converge d’après la règle de Cauchy, c’est-à-dire si, pour n > p, on a

2. Si la série converge d’après la règle de d’Alembert, c’est-à-dire si, pour n > p, 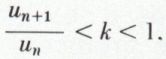on a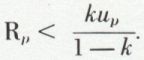

Pratiquement, pour calculer la somme d’une série à près, on calcule les termes, à partir du premier, jusqu’à ce que les n + 2 premières décimales de ces termes soient nulles. Si u_p+1 est le premier terme pour lequel cela se produit, on calcule la somme S_p des p premières valeurs approchées calculées ; pour chacune de ces valeurs, l’erreur est inférieure à l’erreur totale est donc inférieure à On évalue alors une limite supérieure, α_p, du reste R_p, et si, ce qui se produit souvent,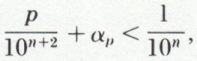

S_p est la valeur approchée cherchée. Cette méthode appliquée au calcul de

donne e = 2,718 281 8, avec sept décimales exactes.

• Si une série à termes quelconques est absolument convergente, c’est-à-dire si la série des valeurs absolues converge, on a | R_p | < R′_p, R′_p, étant le reste de la série des valeurs absolues correspondante.

• Si une série alternée converge d’après le théorème spécial aux séries alternées, on a | R_p | < | u_p+1 |, u_p+1 étant le premier terme négligé de la série.