vecteur (suite)
Moment d’un glisseur par rapport à un axe
• Le comoment de deux glisseurs 
et 
est le produit mixte 
Il est égal au produit scalaire 
étant le moment en A1 du vecteur 
(fig. 13). Il est aussi égal à 
c’est-à-dire au produit scalaire 
du vecteur et du moment en A2 du vecteur 
. On voit ainsi la symétrie de la définition du comoment de deux vecteurs. D’après les propriétés des déterminants, O étant un point quelconque, on a les relations
et 
désignant respectivement les moments des vecteurs et en O. Le comoment des deux vecteurs et est donc indépendant des points A1 et A2, ce qui justifie la définition. Le comoment est scalaire et non un vecteur.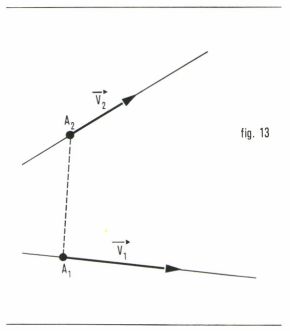
• Le moment d’un glisseur par rapport à un axe est le comoment de ce glisseur et du vecteur unitaire 
de l’axe. Le vecteur unitaire de l’axe est en effet un glisseur. Le vecteur 
étant le moment de 
en O (fig. 14), le comoment de 
et de 
est le produit scalaire de et de . C’est donc la mesure algébrique 
sur le vecteur unitaire de la projection orthogonale 
du vecteur sur l’axe (Δ). Cette mesure algébrique est indépendante du point O choisi, d’après les propriétés du comoment de deux vecteurs.
Systèmes finis de glisseurs
Des glisseurs 
en nombre fini constituent un système fini de glisseurs. Les éléments de réduction d’un système (S) en un point O quelconque de l’espace euclidien de dimension trois sont les deux vecteurs liés suivants :
• 
appelé vecteur somme en O du système (S), égal à la somme des n vecteurs ;
• , appelé moment résultant en O du système (S), égal à la somme des moments 
des vecteurs .
Si O′ est un point de l’espace distinct de O, le vecteur somme en O′ est 
Le moment résultant en O′ est
Cette dernière relation montre qu’on peut calculer le moment résultant en tout point si l’on connaît le moment résultant en un point déterminé et le vecteur somme. D’autre part, il existe deux invariants pour le système (S) : l’un est le vecteur somme 
l’autre est le produit scalaire
puisque le produit vectoriel 
est perpendiculaire au vecteur 
donc au vecteur 
et qu’ainsi le produit scalaire 
est nul.
Systèmes équivalents, torseurs
La connaissance des éléments de réduction d’un système en un point de l’espace entraîne la connaissance de ces éléments en n’importe quel autre point. Deux systèmes (S) et (S′) ayant mêmes éléments de réduction en un point ont mêmes éléments de réduction en tout point. Dans l’ensemble des systèmes finis de glisseurs, la relation binaire a mêmes éléments de réduction que est une relation d’équivalence. Deux systèmes ayant mêmes éléments de réduction sont dits équivalents. Ce sont deux représentants distincts d’une même classe d’équivalence, appelée torseur. Pour que deux systèmes soient représentants d’un même torseur, il faut et il suffit qu’ils aient même moment en tout point. La condition est évidemment nécessaire. Inversement, si les deux systèmes (S) et (S′) ont même moment en tout point, le système (S) – (S′) a un moment nul en tout point. De la relation 
donnant le moment résultant du système (S) – (S′), on tire 
quels que soient les points O et O′. D’où 
et les vecteurs sommes des deux systèmes (S) et (S′) sont égaux puisque (S) – (S′) a un vecteur somme nul.
Axe central d’un torseur
C’est l’ensemble des points de l’espace en lesquels le moment résultant est colinéaire au vecteur somme. Cet ensemble est une droite. Analytiquement, un torseur est défini par son vecteur somme 
et son moment résultant 
en O, LX + MY + NZ étant invariant dans tout l’espace euclidien réel de dimension trois rapporté à une base orthonormée 
Au point M (x, y, z), les composantes du moment résultant sont
L′ = L – yZ + zY, M′ = M – zX + xZ, N′ = N – xY + yX.
Si le vecteur somme n’est pas nul, les équations de l’axe central sont
traduisant la proportionnalité des composantes des vecteurs somme et moment résultant en un point. Ces équations sont au nombre de deux. Elles sont linéaires en x, y et z. Ce sont les équations de deux plans, donc d’une droite.
Torseurs particuliers
• Un torseur nul est un torseur dont les éléments de réduction en un point, donc en tout point, sont nuls.
• Un torseur-couple est un torseur ayant même moment en tout point de l’espace. Les deux glisseurs 
et 
ont pour vecteurs associés deux vecteurs libres opposés (fig. a). Le vecteur somme du système formé par les vecteurs et est nul. Le moment en A du vecteur est nul, car A est sur le support (Δ1) du vecteur . Le moment en A du vecteur est 
AH étant perpendiculaire à (Δ1) et (Δ2). Ce moment est indépendant du point A choisi sur le support (Δ1). En un point A′ quelconque de l’espace, le moment est
puisque 
Le moment du système formé par les vecteurs et est le même en tout point de l’espace ; 
est un torseur-couple. Inversement (fig. b), si (S) est un système ayant même moment en tout point, ce moment, en un point A, est 
. On choisit un vecteur 
, d’origine A, perpendiculaire à . La droite AH est perpendiculaire aux vecteurs et . La demi-droite AH est telle que le trièdre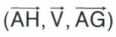 
soit direct. La longueur AH a pour valeur 
Le point H est ainsi déterminé. La droite (Δ2) est la parallèle au vecteur passant par le point H. Le vecteur glissant de support (Δ2), ayant pour vecteur associé le vecteur , a pour moment en A le vecteur . Le vecteur , de support (Δ1) et opposé au vecteur , a un moment nul en A. Le système 
formé par les vecteurs et a même moment que le système (S) en tout point de l’espace, ce moment étant équipollent au vecteur . Les deux systèmes sont donc équivalents. Ainsi, un torseur-couple est équivalent au système formé de deux glisseurs associés à des vecteurs opposés. Les torseurs-couples sont les torseurs dont le vecteur somme est nul.
E. S.
E. S.
➙ Déterminant / Espace euclidien de dimension trois / Géométrie / Vectoriel sur un corps commutatif.
H. Blanchard et C. Forest, Traité de mathématiques, t. II (Hachette, 1967). / G. Cagnac, E. Ransis et J. Commeau, Traité de mathématiques spéciales, t. III : Géométrie (Masson, 1971).