vecteur (suite)
Multiplication d’un vecteur par un nombre réel
Le module du vecteur  est un nombre réel positif ; on le désigne par
est un nombre réel positif ; on le désigne par 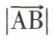 ou par AB. Étant donné un réel quelconque α, on désigne par
ou par AB. Étant donné un réel quelconque α, on désigne par 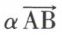 le vecteur lié d’origine A, dont le support est AB, dont le module est |α| AB et dont le sens est celui du vecteur
le vecteur lié d’origine A, dont le support est AB, dont le module est |α| AB et dont le sens est celui du vecteur  si α > 0 ou celui du vecteur
si α > 0 ou celui du vecteur 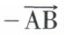 si α < 0, soit
si α < 0, soit 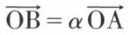 (fig. 6).
(fig. 6).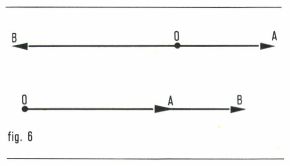
Si  désigne le vecteur libre dont le vecteur
désigne le vecteur libre dont le vecteur  est un représentant,
est un représentant, 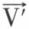 celui dont le vecteur
celui dont le vecteur 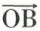 est un représentant, on écrit
est un représentant, on écrit 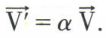
La multiplication des vecteurs libres par un scalaire est une opération externe pour l’ensemble des vecteurs libres. Si 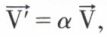 on dit que les vecteurs
on dit que les vecteurs  et
et 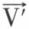 sont colinéaires, comme le sont réellement deux représentants de
sont colinéaires, comme le sont réellement deux représentants de  et de
et de 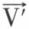 , qui ont même origine.
, qui ont même origine.
Si α et β sont deux réels quelconques,  et
et 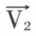 deux vecteurs quelconques de l’espace, on a les relations suivantes :
deux vecteurs quelconques de l’espace, on a les relations suivantes :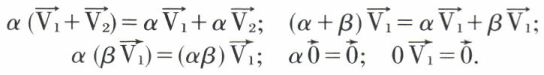
La première relation traduit la distributivité de la multiplication, par un scalaire, par rapport à l’addition vectorielle ; la deuxième, celle de la multiplication par rapport à l’addition des réels ; la troisième, une associativité partielle.
L’ensemble des vecteurs libres muni de l’addition vectorielle et de la multiplication par un scalaire réel a une structure d’espace vectoriel sur ℝ, ensemble des réels. Dans cet espace vectoriel, deux vecteurs non nuls et non colinéaires sont linéairement indépendants. Trois vecteurs non nuls et coplanaires sont linéairement dépendants (fig. 7) : 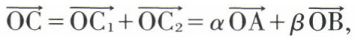 car, d’une part, les vecteurs
car, d’une part, les vecteurs 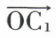 et
et  , et, d’autre part, les vecteurs
, et, d’autre part, les vecteurs 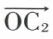 et
et 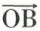 sont colinéaires. Trois vecteurs non nuls et non coplanaires sont linéairement indépendants. Quatre vecteurs non nuls sont linéairement dépendants.
sont colinéaires. Trois vecteurs non nuls et non coplanaires sont linéairement indépendants. Quatre vecteurs non nuls sont linéairement dépendants.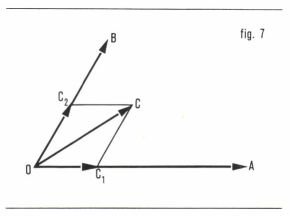
Glisseurs
Un vecteur glissant, ou glisseur, est une classe d’équivalence dans l’ensemble des vecteurs liés muni de la relation d’équivalence avoir même support et être équipollents. Un glisseur est donc défini par un vecteur libre et une droite qui est le support du glisseur : on note  le glisseur défini par le vecteur libre
le glisseur défini par le vecteur libre  et par le point A de son support, lequel est parallèle à
et par le point A de son support, lequel est parallèle à  (fig. 8).
(fig. 8).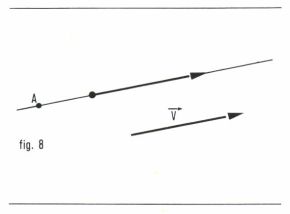
Opérations sur les glisseurs
Les deux glisseurs  et
et 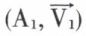 sont égaux si et seulement si
sont égaux si et seulement si 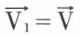 et si la droite AA1 a la direction du vecteur
et si la droite AA1 a la direction du vecteur  .
.
• La somme de deux glisseurs est définie si leurs supports sont concourants. Dans ce cas, on a la relation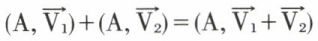 (fig. 9).
(fig. 9).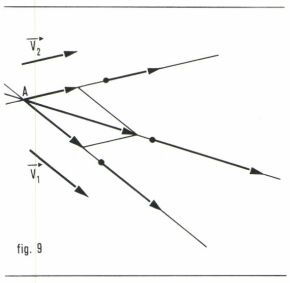
• Le produit d’un glisseur  par un scalaire réel α est le glisseur
par un scalaire réel α est le glisseur 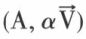 ou a
ou a 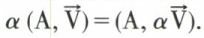 Ce dernier glisseur est parfaitement défini.
Ce dernier glisseur est parfaitement défini.
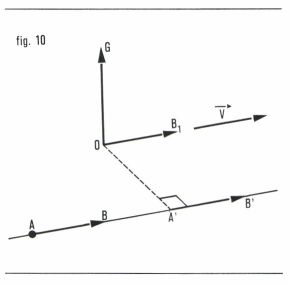
Moment d’un glisseur en un point
Le moment en un point O (fig. 10) du vecteur glissant  est le vecteur lié
est le vecteur lié  produit vectoriel des deux vecteurs
produit vectoriel des deux vecteurs  et
et  . Ce vecteur lié
. Ce vecteur lié  est indépendant du point A, car, si A′ est un autre point du support du glisseur
est indépendant du point A, car, si A′ est un autre point du support du glisseur  , on a
, on a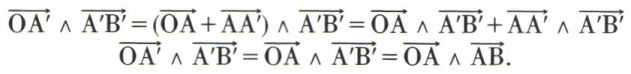
En effet, le produit vectoriel 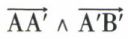 est nul, puisque les vecteurs
est nul, puisque les vecteurs  et
et  sont colinéaires. Le moment est donc indépendant de l’origine choisie sur le support du glisseur, ce qui justifie la définition du moment et même l’étude des glisseurs. On peut, en particulier, prendre comme point A′ la projection orthogonale du point O sur le support du glisseur. Le module du vecteur
sont colinéaires. Le moment est donc indépendant de l’origine choisie sur le support du glisseur, ce qui justifie la définition du moment et même l’étude des glisseurs. On peut, en particulier, prendre comme point A′ la projection orthogonale du point O sur le support du glisseur. Le module du vecteur  est égal au produit des longueurs OA′ et A′B′. Le trièdre déterminé par les trois vecteurs
est égal au produit des longueurs OA′ et A′B′. Le trièdre déterminé par les trois vecteurs 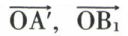 et
et  est direct, avec
est direct, avec 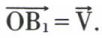 Le moment
Le moment  est perpendiculaire au plan déterminé par le point O et le support du glisseur quand ce point O n’appartient pas à ce support.
est perpendiculaire au plan déterminé par le point O et le support du glisseur quand ce point O n’appartient pas à ce support.
Si le point O est sur le support du glisseur, le moment en ce point est nul.
Si O′ est un point quelconque distinct du point O, le moment en O′ est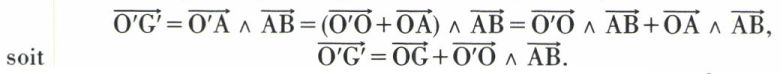
Cette relation permet de calculer le moment en O′, connaissant le moment en O et le vecteur libre associé au glisseur. D’ailleurs, il est possible de déterminer un glisseur dont on connaît le moment  en un point O et le vecteur associé
en un point O et le vecteur associé  , à condition que les deux vecteurs
, à condition que les deux vecteurs  et
et  soient orthogonaux.
soient orthogonaux.
Si 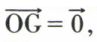 le support du glisseur est la droite passant par le point O et parallèle au vecteur
le support du glisseur est la droite passant par le point O et parallèle au vecteur  (fig. 11).
(fig. 11).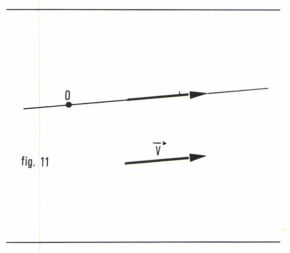
Si 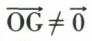 (fig. 12), le support cherché est dans le plan (P) passant par le point O et perpendiculaire au vecteur
(fig. 12), le support cherché est dans le plan (P) passant par le point O et perpendiculaire au vecteur  . Le trièdre
. Le trièdre 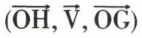 devant être direct, le point H ne peut appartenir qu’à l’un des deux demi-plans déterminé, dans (P), par la parallèle au vecteur
devant être direct, le point H ne peut appartenir qu’à l’un des deux demi-plans déterminé, dans (P), par la parallèle au vecteur  passant par le point O. D’autre part, la distance OH du point O au support cherché est telle que
passant par le point O. D’autre part, la distance OH du point O au support cherché est telle que 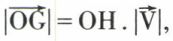 ce qui détermine d’abord la longueur
ce qui détermine d’abord la longueur 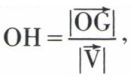 puis le point H, puisque l’angle (OH, OV) est droit : d’où le support passant par le point H et perpendiculaire à OH.
puis le point H, puisque l’angle (OH, OV) est droit : d’où le support passant par le point H et perpendiculaire à OH.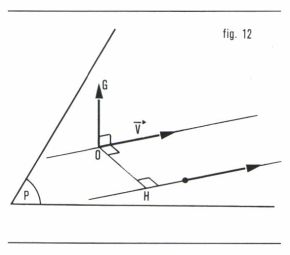
Détermination analytique d’un glisseur
L’espace euclidien est rapporté à un repère orthonormé 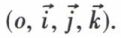 Le glisseur
Le glisseur  est défini par les coordonnées (x, y, z) du point A et les composantes du vecteur libre
est défini par les coordonnées (x, y, z) du point A et les composantes du vecteur libre 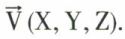 Le moment en O,
Le moment en O, 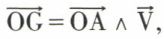 a pour composantes
a pour composantes
L = yZ – zY, M = zX – xZ, N = xY – yX,
entre lesquelles existe la relation LX + MY + NZ = 0, ce qui traduit analytiquement, à l’aide du produit scalaire  .
.  , que le vecteur
, que le vecteur  est orthogonal au vecteur
est orthogonal au vecteur  .
.
Inversement, on peut se donner un glisseur par son moment en O,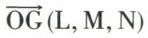
et son vecteur associé 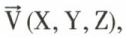 tels que
tels que 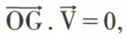 ou LX + MY + NZ. Le support du glisseur est l’ensemble des points M (x, y, z) tels que
ou LX + MY + NZ. Le support du glisseur est l’ensemble des points M (x, y, z) tels que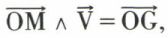
c’est-à-dire tels que
yZ – zY = L, zX – xZ = M, xY – yX = N.
Ces trois équations sont compatibles, car LX + MY + NZ = 0 ; elles se réduisent donc à deux équations de plans définissant une droite, support du vecteur glissant étudié.




