thermodynamique (suite)
Si, d’abord, on ne considère que des transformations réversibles, l’entropie présente le même caractère de conservation que les autres extensités : masse, charge électrique, etc. Dans une machine thermique réversible, au bout d’un cycle, la source chaude a cédé l’entropie Q1/T1, et la source froide a reçu l’entropie
q2/T2 = – Q2/T2 ;
puisque Q1/T1 + Q2/T2 = 0, on voit que de l’entropie a été simplement transférée de la source chaude à la source froide. Quant au système, qui est revenu à l’état initial après ces seuls échanges de chaleur, son entropie n’a pas varié au total : il a reçu de la source chaude l’entropie Q1/T1, il a cédé à la source froide une égale entropie – Q2/T2, et, dans les intervalles de contact avec les sources, son entropie est restée la même, car les transformations adiabatiques réversibles sont isentropiques.
D’une façon plus générale, lorsqu’un système accomplit par voie entièrement réversible un cycle au cours duquel il échange des quantités de chaleur ΔQ1, ΔQ2, ..., ΔQn avec des sources de températures T1, T2, ..., Tn, on a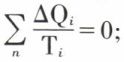 
si, à la limite, le nombre des sources augmente indéfiniment et si chaque ΔQ tend vers zéro, 
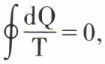tant pour le système que pour l’ensemble des sources. Il en résulte que, si l’on considère le passage d’un système d’un état 1 à un état 2, la variation de l’entropie, mesurée par 
est bien déterminée et ne dépend que de l’état initial et de l’état final : l’entropie S d’un système est une fonction des variables qui définissent son état. On peut dire aussi que, pour une transformation infiniment petite, dS = dQ/T est différentielle totale (1/T est le facteur intégrant de dQ). C’est là, de façon analogue au premier principe, une expression mathématique du deuxième principe, efficace pour les applications.
Ainsi, l’entropie se conserve au cours des transformations réversibles ; il n’en est plus de même dans les transformations réelles, lesquelles comportent toujours une part d’irréversibilité. Dans le moteur ditherme réel, l’échange de chaleur entre la source chaude et le système qui évolue exige que ce dernier soit à une température 
inférieure à la température T1 de la source chaude : celle-ci cède l’entropie Q1/T1, mais le système reçoit l’entropie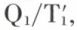 
supérieure à Q1/T1. Il en va de même au contact de la source froide : celle-ci reçoit l’entropie q2/T2, alors que le système cède l’entropie 
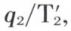avec 
d’où 
et la source froide reçoit plus d’entropie que n’en cède le système. Ce dernier revenant au bout d’un cycle à son état initial, son entropie reprend la même valeur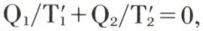 
et, par suite, Q1/T1 + Q2/T2 < 0, ce qui signifie, en passant aux chaleurs reçues par les sources, que celles-ci ont, dans l’ensemble, gagné de l’entropie au cours d’un cycle ; l’entropie du système total a donc augmenté. On verrait qu’il en est de même quelles que soient les causes d’irréversibilité : frottements, effet Joule... ; on dit que l’irréversibilité est créatrice d’entropie.
Un système isolé, s’il n’est pas en équilibre, c’est-à-dire s’il existe à l’intérieur des différences de température, de pression, des réactions chimiques possibles, etc., est le siège d’une évolution interne, au cours de laquelle son énergie interne demeure constante ; son entropie, par contre, ne peut qu’augmenter ; en même temps, la part de l’énergie interne transformable en travail diminue ; elle s’annule lorsque l’entropie a atteint sa valeur maximale et qu’un équilibre définitif est atteint. C’est cette croissance inéluctable de l’entropie qui a fait dire que, du point de vue macroscopique auquel se place la thermodynamique, un système isolé ne peut passer deux fois par le même état.
Troisième principe
Nernst*, frappé de ce que l’expérience vérifie d’autant mieux le principe du travail maximum de Berthelot* (v. thermochimie) que la température est plus basse, fut amené (1906) à considérer que les variations ΔH et ΔG = ΔH – T · ΔS de l’enthalpie H et de l’enthalpie libre G, relatives à une transformation isotherme d’un système, tendent à devenir égales quand la température thermodynamique tend vers zéro. De là résulte le postulat de Nernst, suivant lequel l’entropie de tous les éléments tend, lorsque T tend vers zéro, vers une limite finie, indépendante de la pression, de l’état allotropique et de l’état de combinaison de ces éléments.
Planck* a ajouté à ce postulat la convention suivant laquelle la valeur de l’entropie est prise égale à zéro pour tous les corps, à T = 0.
Les conséquences du postulat de Nernst-Planck sont nombreuses et importantes. D’abord, on peut montrer que le postulat est cohérent avec le principe de l’inaccessibilité du zéro de l’échelle thermodynamique des températures. Ensuite, en supprimant la constante dans l’expression de l’entropie d’un corps en fonction de ses variables d’état, il simplifie le maniement des fonctions caractéristiques, principalement F et G, et permet le calcul d’une constante d’équilibre chimique à partir de données thermochimiques et calorimétriques, dont il existe des tables ; les résultats expérimentaux obtenus dans ce domaine apportent au troisième principe une confirmation ainsi, d’ailleurs, que la décroissance rapide, bien étudiée expérimentalement, des chaleurs massiques* des solides quand la température s’abaisse. On peut remarquer que le modèle classique du gaz parfait ne satisfait pas au troisième principe ; mais ce modèle, satisfaisant aux températures élevées, ne l’est plus aux basses températures et doit faire place à un modèle quantique ; les résultats de la thermodynamique statistique, dans ses versions quantiques, sont d’accord avec le troisième principe. Quant aux gaz réels, ils sont tous condensés à température suffisamment faible.
Application des principes
Les principes permettent de définir pour un système son énergie interne U et son entropie S en fonction de variables d’état indépendantes. Dans une transformation infiniment petite éprouvée par le système, on exprimera les principes en écrivant que, d’une part, dU et, d’autre part, dS sont différentielles totales, ce qui fournit un certain nombre de relations. Ainsi, dans le cas d’un fluide homogène, dont l’état, en raison de l’existence d’une équation d’état, dépend de deux variables seulement, on est conduit (v. coefficients thermodynamiques) aux expressions des chaleurs latentes de compression et de détente 
et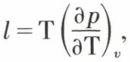 
calculables dès lors à l’aide de l’équation d’état du fluide et qui constituent des formules de Clapeyron. On obtient aussi une expression très importante de la différence des chaleurs spécifiques du fluide
calculable, elle aussi, à partir de l’équation d’état et qui, dans le cas du gaz parfait, conduit à la célèbre relation de R. Mayer Cp – Cv = R. Le même procédé de calcul est applicable pour l’étude, dans divers domaines de la physique, de la mécanique, de l’électricité..., de phénomènes tels que la variation d’état du système peut être exprimée à l’aide de deux variables indépendantes seulement, ce qui est un minimum de complexité. Cependant, il est parfois plus simple, pour appliquer le deuxième principe, de faire appel dans le raisonnement au cycle de Carnot, auquel correspond, d’après le théorème de Carnot, le rendement 1 – T2/T1 lorsque la différence de température des sources chaude et froide est finie, et dT/T lorsque cette différence est infiniment petite. On peut ainsi retrouver les formules de Clapeyron (v. vaporisation) ou encore montrer que l’échelle absolue des gaz parfaits coïncide avec une échelle thermodynamique de températures (v. température).