symétrie (suite)

• Produits de deux symétries par rapport à deux plans
Les deux plans sont sécants (fig. 7). Le point M est transformé en un point M₁ par la symétrie S_P, lequel est transformé en un point M′ par la symétrie S_P′ ; le point M est transformé en M′ par le produit S_P′ ∘ S_P. Les trois points M, M₁ et M′ appartiennent au plan (π) passant par le point M et perpendiculaire à la droite (Δ) d’intersection des plans (P) et (P′). Dans ce plan, on passe du point M au point M′ par la rotation de centre O et d’angle et étant deux axes arbitrairement choisis sur les traces (D) et (D′) des plans (P) et (P′) sur le plan (π). L’angle obtenu dans (π) est indépendant du point M choisi. On retrouve le même angle si on part d’un point M non situé dans (π) : c’est le rectiligne, ou angle plan, de l’un des dièdres orientés formés par les plans (P) et (P′). Le produit S_P ∘ S_P est une rotation dont l’angle est égal à et dont l’axe, porté par (Δ), a un sens convenable. Inversement, une rotation d’angle α autour d’un axe peut être décomposée d’une infinité de manières en un produit de deux symétries-plans dont les plans passent par l’axe , l’un des dièdres déterminés par ces plans ayant un rectiligne orienté de mesure

• Les plans sont parallèles (fig. 8). On passe du point M au point M′ par le produit S_P′ ∘ S_P, qui est ici une translation, dont le vecteur est double de celui de la translation qui transforme le plan (P) en (P′). Inversement, une translation de vecteur peut être décomposée d’une infinité de façons en un produit de deux symétries-plans dont les plans sont perpendiculaires à la direction du vecteur et dont l’un se déduit de l’autre par la translation de vecteur

Dans les deux cas ci-dessus, on obtient comme produit de deux symétries-plans un déplacement.

Symétrie par rapport à une droite

Cette transformation, appelée aussi retournement (fig. 9), n’est autre que la rotation involutive d’axe porté par la droite (Δ), de sens arbitraire. Une symétrie par rapport à une droite dans l’espace est un déplacement. Deux figures d’un même plan symétriques par rapport à une droite (Δ) de ce plan sont inversement égales dans ce plan (fig. 10), mais sont directement égales dans l’espace. On passe de l’une à l’autre par le retournement d’axe (Δ).

• Produit de deux retournements
Les deux axes sont parallèles (fig. 11). Les deux droites parallèles (Δ₁) et (Δ₂) déterminent un plan (P). Soit (Q) et (R) les plans contenant respectivement les droites (Δ₁) et (Δ₂), perpendiculaires au plan (P). On peut décomposer les symétries par rapport aux deux droites (Δ₁) et (Δ₂) en produits de deux symétries-plans : 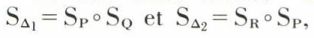de sorte que

ou puisque S_P ∘ S_P = I (identité).

Or, le produit S_R ∘ S_Q est la translation de vecteur étant le vecteur de la translation transformant (Q) en (R).

Le produit de deux retournements d’axes parallèles est la translation de vecteur double de celui qui transforme un axe en l’autre.

• Les deux axes sont concourants (fig. 12). Comme précédemment, on décompose chaque retournement en un produit de deux symétries par rapport à deux plans perpendiculaires d’où

Or, le produit S_R ∘ S_Q de deux symétries par rapport à deux plans concourants est une rotation autour de la droite d’intersection de ces deux plans.

Le produit de deux retournements d’axes concourants est une rotation d’axe perpendiculaire au plan déterminé par les deux axes, en leur point commun, l’angle de la rotation étant le double de l’angle des deux axes.

Symétrie par rapport à un point

Cette transformation associe à tout point M de l’espace le point M′ tel que O étant un point donné. C’est aussi une homothétie de centre O et de rapport – 1, donc un antidéplacement, puisque les distances sont conservées, mais les trièdres sont remplacés par des trièdres de sens contraires.
1. Le produit de la symétrie de centre O et de la symétrie de centre O′ est la translation de vecteur
2. La symétrie de centre O peut être remplacée, dans un ordre quelconque, par le produit de la symétrie par rapport à un plan (P) quelconque passant par le point O et du retournement d’axe (Δ) perpendiculaire au plan (P) en O ou par le produit de trois symétries par rapport à trois plans deux à deux perpendiculaires et passant par le point O.

Il résulte de ces propriétés que :
1^o si une figure admet, parmi l’ensemble formé d’un plan, d’un point de ce plan et de la perpendiculaire en ce point au plan, deux de ces éléments comme éléments de symétrie, elle admet aussi le troisième ;
2^o si une figure admet trois plans de symétrie deux à deux perpendiculaires, elle admet leur point commun comme centre de symétrie et les droites d’intersection des plans deux à deux, comme axes de symétrie.

Groupe des isométries de l’espace euclidien

L’ensemble des isométries de l’espace, c’est-à-dire des déplacements et des symétries par rapport à des points ou à des plans, est un groupe non commutatif pour la composition des transformations. L’ensemble formé des déplacements de l’espace est un sous-groupe du groupe des isométries.

Toute isométrie de l’espace est égale soit à la transformation identique, soit à une symétrie-plan, soit au produit de deux, de trois ou de quatre symétries-plans.