suite de nombres réels (suite)
Exemple. 
, où (εn) est une suite de nombres égaux à 1 ou à – 1. Pour p > q,
Par suite,
La suite (xn) est une suite de Cauchy. Elle converge donc dans ℝ vers une limite l que l’on peut encadrer.
En effet 
et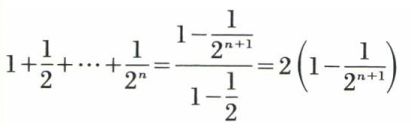 
tend vers 2 par valeurs inférieures quand n → + ∞, en croissant. Il en résulte que 
• La suite (yn) est dite équivalente à la suite (xn) s’il existe une suite (αn) tendant vers 1, telle que, pour n > n0, yn = αnxn. Si la suite (xn) est convergente, il en est de même de la suite (yn). Inversement, si (xn) et (yn) sont deux suites convergeant vers une même limite non nulle, elles sont équivalentes.
Exemple. Les suites 
sont équivalentes.
• La limite d’une suite de Cauchy est unique. Si (xn) est à termes positifs ou nuls, sa limite est positive ou nulle. Si la limite l de la suite (xn) à termes positifs ou nuls était négative, pour n > nε, on aurait |l – xn| < ε, ce qui signifie que tous les termes de (xn) sont négatifs si l’on prend ε = |l|. Ce qui est faux. Donc l = 0.
Comme conséquence, si (xn) et (yn) sont deux suites convergeant respectivement vers l et l′, et si, pour tout n, 
alors 
En effet, la suite (zn) = (xn – yn), à termes positifs ou nuls, a une limite positive ou nulle qui est égale à l – l′.
• Si les suites (xn) et (yn) convergent respectivement vers l et l′, la suite (zn) = (xn + yn) converge vers l + l′. Si la suite (xn) tend vers zéro et si la suite (yn) est bornée, la suite (vn) = (xnyn) tend vers zéro. Si la suite (xn) tend vers une limite l non nulle, la suite 
tend vers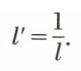 
Suites adjacentes
Si deux suites (xn) et (yn) sont telles que (xn) soit croissante, (yn) décroissante, 
pour tout n ∈ ℕ et xn – yn → 0, ces deux suites ont une limite commune l : 
et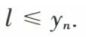 
Les suites (xn) et (yn) sont dites adjacentes.
Exemple. 
La suite (xn) est donc croissante. De plus,
La suite (yn) est donc décroissante. Enfin, on a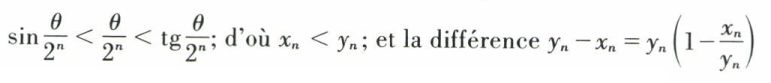
tend vers zéro puisque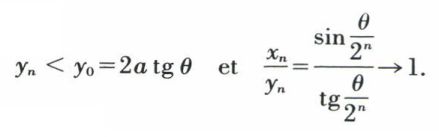
D’où l’existence de la limite commune l = 2a θ, équivalent commun de xn et yn, quand n → + ∞.
Suites monotones
Tout sous-ensemble X majoré (respect, minoré) de ℝ possède une borne supérieure (respect, inférieure), ou plus petit majorant M (respect, plus grand minorant m), telle que :
Il en résulte que :
— toute suite décroissante minorée a une limite finie et toute suite décroissante non minorée tend vers – ∞.
— toute suite décroissante minorée a une limite finie et toute suite décroissante non minorée tend vers – ∞.
Dans le premier cas, quel que soit ε > 0, il existe p ∈ ℕ tel que, l désignant la borne supérieure, 
Pour n > p, xn > xp ; d’où 
ce qui montre que la suite (xn) tend vers l.
Dans le cas d’une suite décroissante, la limite est la borne inférieure.
Ces deux importants théorèmes permettent d’étudier de nombreuses suites.
Exemples. Soit à étudier la suite
Cette suite est croissante. En effet, 
. Supposons xn > xn–1. Alors
Cette suite est majorée par le nombre 2. En effet, 
. Supposons xn < 2. Alors
La suite (xn) a donc une limite positive qui vérifie nécessairement la relation 
l est donc la racine positive de l’équation l2 – l – 2 = 0, c’est-à-dire l = 2.
Plus grande et plus petite limite
À toute suite (xn) de nombres réels, on peut associer deux éléments de ℝ qui généralisent la notion de limite et qui sont égaux à la limite de (xn,) quand (xn) converge.
Plus grande limite ou limite supérieure de la suite (xn)
C’est un élément L de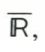 
unique, tel que :
— quel que soit λ < L, l’ensemble des xn qui vérifient xn > λ est infini ;
— quel que soit λ > L, l’ensemble des xn qui vérifient xn > λ est fini.
On note 
Plus petite limite ou limite inférieure de la suite (xn)
C’est un élément l de 
unique, tel que :
— quel que soit λ > l, l’ensemble des xn qui vérifient xn < λ est infini ;
— quel que soit λ < l, l’ensemble des xn qui vérifient xn < λ est fini.
On note 
On a L = + ∞ (respect. l = – ∞) si et seulement si la suite (xn) est non majorée (respect, non minorée).
Pour qu’une suite (xn) soit convergente dans 
il faut et il suffit que L = l, et l’on a
La notion de suite est importante. Le problème des séries numériques, par exemple, revient à l’étude d’une suite formée de la somme des n premiers termes de la série. D’autre part, la plupart des notions précédentes, c’est-à-dire celles qui font appel à la structure d’espace topologique de la droite réelle ℝ, sont susceptibles d’être définies dans un espace topologique E général ou dans un espace métrique E muni d’une distance d. Il en est ainsi de la notion de limite et de celle de suite de Cauchy.
E. S.
➙ ℕ / ℚ / ℝ / Série / Topologie / ℤ.