statique graphique

Ensemble des méthodes qui permettent de résoudre graphiquement les problèmes posés par l’équilibre des systèmes matériels.

La statique graphique concerne les vecteurs parallèles à un même plan. La précision maximale que l’on peut atteindre est de l’ordre du ce qui est en général suffisant. Il s’agit de composer les forces suivant la règle du parallélogramme ou, inversement, de décomposer une force en des composantes suivant des directions données. L’application directe de la méthode générale serait souvent impossible matériellement, car il est rare que les forces concourantes dont on cherche la résultante puissent se couper dans le cadre de l’épure. On applique alors une méthode fondée sur les propriétés du polygone funiculaire.

Polygone dynamique d’un système de forces

En statique graphique, une force est représentée d’une part par sa ligne d’action, d’autre part par un vecteur équipollent à celui qui, sur cette ligne d’action, définirait le sens et l’intensité de la force. Si l’on a un système de trois forces , 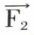et 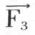, on construit à partir d’un point arbitraire O pris pour origine la résultante de ces trois forces (lignes d’action 1, 2 et 3). De O on mène un vecteur équipollent à , soit , puis de l’extrémité de un vecteur équipollent à 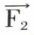, soit , et enfin de l’extrémité de un vecteur équipollent à 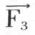, soit . La ligne polygonale est appelée polygone dynamique ou dynamique de F₁F₂F₃. Le vecteur est la résultante . La notion du polygone dynamique suffit à résoudre tous les problèmes d’équilibre relatifs à des systèmes de forces d’un plan concourant en un même point à distance finie : par exemple, étant donné un nombre quelconque de forces appliquées en un même point A, trouver la grandeur et la direction d’une dernière force appliquée au même point A, qui, jointe aux précédentes, assure l’équilibre en ce point. On construit le dynamique et l’on prend comme force équilibrante la résultante changée de signe.

Polygone funiculaire d’un système de forces

Étant donné trois forces , , 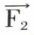, 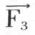définies par leurs lignes d’action 1, 2, 3 et leur dynamique d₀d₁d₂d₃, si l’on joint un point quelconque P du plan, pris pour pôle, aux sommets de ce dynamique par les rayons polaires 0′, 1′, 2′, 3′ et que l’on construise une ligne polygonale f₀ f₁ f₂ f₃ f₄, dont les côtés 0′, 1′, 2′, 3′ soient parallèles aux rayons polaires du même numéro et dont les sommets se trouvent sur les lignes d’action ayant pour numéro l’indice correspondant, cette ligne polygonale est un polygone funiculaire des forces , , 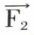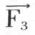. Pour une position donnée du pôle P, tous les funiculaires ont leurs côtés homologues deux à deux parallèles.

Propriété fondamentale des quadrangles réciproques

Deux figures réciproques sont des configurations de droites telles qu’il y ait parallélisme entre droites correspondantes, mais avec la condition qu’à des droites concourantes sur l’une des figures correspondent des droites non concourantes sur la seconde, et réciproquement.

Quand deux quadrangles non semblables sont tels que cinq des six droites joignant leurs quatre sommets deux à deux se groupent de l’un à l’autre par couples parallèles, ces quadrangles sont réciproques, et les sixièmes droites sont également parallèles entre elles. On déduit de ce lemme que les côtés correspondants de deux funiculaires pour un même système de forces, mais avec deux pôles différents, se coupent deux à deux sur une même droite Δ, parallèle à celle qui unit les deux pôles. On dit alors que les deux funiculaires sont en relation d’homologie, la droite Δ étant l’axe d’homologie.

Détermination de la résultante d’un système quelconque de forces coplanaires

La résultante des forces , , 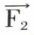, 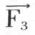est toujours donnée en grandeur et en sens par le vecteur directement opposé à celui qui ferme le dynamique (vecteur n^o 4). Pour trouver un point de la ligne d’action de cette résultante, on applique le long de chacun des côtés du funiculaire f₀ f₁ f₂ f₃ f₄ deux forces égales et opposées ayant pour vecteurs équipollents les rayons polaires correspondants pris en l’un et l’autre sens, par exemple le long de f₀ f₁, deux forces équipollentes et et ainsi de suite. On peut ainsi grouper en chacun des sommets du funiculaire trois forces se faisant équilibre. Par exemple : en f₁, des forces dirigées suivant les lignes d’action 0′, 1 et 1′, équipollentes à et en f₂, des forces dirigées suivant les lignes d’action 1′, 2 et 2′, équipollentes à et et ainsi de suite. Les forces appliquées en chaque sommet, se faisant équilibre, puisque leur dynamique est fermé, peuvent être supprimées. Finalement, il ne reste que la force équipollente à dirigée suivant f₃ f₄. La résultante passe donc par le point de rencontre θ de ces deux lignes d’action, c’est-à-dire par le point de rencontre des côtés extrêmes du funiculaire.

Cas des forces parallèles. Centre de gravité d’un système de points

Le dynamique se réduit alors à une droite d₀d₃ parallèle à la direction commune des forces ; le funiculaire d₀d₁d₂d₃d₄, ayant P pour pôle, donne, pour la rencontre de ses côtés extrêmes, un point θ de la ligne d’action de la résultante, laquelle est parallèle aux composantes et de grandeur égale à d₀d₃. On en déduit une construction du centre de gravité G d’un système de points A₁A₂A₃ affectés de poids donnés par les vecteurs , et du dynamique. Ce centre de gravité se trouve d’abord sur la ligne d’action menée par θ. Si on fait tourner toutes les lignes d’action , , d’un même angle respectivement autour des points A₁, A₂, A₃, la ligne d’action de la nouvelle résultante contient également le point G, qui est à l’intersection des deux résultantes. On peut adopter comme angle de rotation un angle droit ; et, comme le pôle P est arbitraire, on peut, en conservant ce même pôle P, faire effectuer au dynamique primitif une rotation de π/2 autour de ce pôle : les nouvelles positions des divers rayons polaires sont normales aux côtés correspondants de l’ancien dynamique ; on tracera successivement le côté φ₀φ₁, perpendiculaire à f₀f₁, le côté φ₁φ₂, perpendiculaire à f₁f₂, etc. La parallèle à la ligne d’action menée par le point de rencontre θ′ des côtés φ₀φ₁ et φ₃φ₄ coupe la ligne d’action primitivement menée par le point θ au centre de gravité cherché.

• Détermination du centre de gravité d’une aire plane. On applique le procédé précédent, en décomposant l’aire en aires élémentaires.