Éléments universels

Un programme écrit avec les quatre instructions introduites lors de la définition par programme des fonctions récursives peut être considéré comme une écriture finie sur un alphabet fini X. Toutefois, un programme n’est pas une suite finie quelconque d’éléments de X. Il faut respecter certaines règles de syntaxe pour qu’une suite finie d’éléments de X soit bien formée ou corresponde à un programme. Si d’autre part l’on considère une « bonne » bijection entre L (X) et ℕ et si l’on désigne dans ces conditions par A ⊂ ℕ l’ensemble des nombres correspondant à l’écriture d’un programme dans cette bijection, si celle-ci possède une propriété naturelle (le fait que la concaténation soit représentée par une application récursive), l’ensemble A est récursif. Il existe un procédé mécanique donné par les règles de syntaxe permettant de reconnaître si oui ou non un nombre quelconque appartient à l’ensemble A, c’est-à-dire correspond dans cette bijection à l’écriture d’un programme.

Soit alors l’application définie de la façon suivante :

u^(p) désignant l’élément de *F^(p) tel que u^(p) (x) = u pour tout x ∈ ℕ^p.

L’application φ peut être considérée comme une application à (p + 1) arguments en posant pour tout x, x₁, ..., x_p ∈ ℕ (x, x₁, ..., x_p) = φ (x) (x₁, ..., x_p).

Cette application appartient à 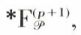c’est-à-dire qu’il existe un algorithme permettant de passer de (x, x₁, ..., x_p) à (x, x₁, ..., x_p). Cet algorithme consiste d’abord à reconnaître si x ∈ A ou non, ce qui est possible de façon mécanique. Si alors x ∉ A, (x, x₁, ..., x_p) = u, et on effectue dans ce cas un programme ne s’arrêtant jamais, par exemple celui qui est composé de la seule instruction q₁ : T (q₁, q₁) (0).

Si x ∈ A, par définition de φ, (x, x₁, ..., x_p) s’obtient par application du programme de numéro x sur les arguments x₁, ..., x_p. L’algorithme qu’il faudrait décrire a pour but, dans ce cas, d’appliquer un programme quelconque sur ses arguments. Il n’est pas évident, à première vue, qu’un tel algorithme existe. Toutefois, si l’on considère les machines électroniques à programmes enregistrés, on constate que le principe de fonctionnement de ces machines consiste effectivement à appliquer un programme sur ces arguments. On connaît donc l’existence d’un mécanisme concret susceptible de réaliser cette tâche, et l’on peut admettre, en vertu de la thèse de A. Church, que sa description peut être explicitée dans le langage à quatre instructions utilisé pour la définition de Ainsi, le principe de calcul de correspond essentiellement à celui des ordinateurs modernes.

Cet élément est qualifié d’universel et possède de très nombreuses propriétés intéressantes : théorème de récursion de S. C. Kleene, théorème de Rice, de Hartley Rogers, et J. Myhill, etc. On l’utilise notamment pour construire un ensemble récursivement énumérable non récursif. Le procédé de construction, la « diagonalisation », est une des méthodes les plus utilisées en récursivité classique.

On remarque d’abord qu’un ensemble récursif est récursivement énumérable et que le complémentaire d’un ensemble récursif est récursif. Soit alors un élément universel et soit K = {x/φ (x, x) ≠ u}. L’ensemble K est récursivement énumérable, car il est le domaine de définition de f ou f (x) = φ (x, x), pour tout x ∈ ℕ, et f appartient à 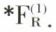Si l’ensemble K est récursif, son complémentaire ∁_K l’est également, et, par suite, ∁_K est récursivement énumérable. Donc il existe 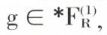tel que ∁_K = dom g. Mais l’élément φ étant universel, l’application φ en tant qu’application de ℕ dans 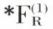est surjective par construction. Par suite, il existe n₀ ∈ ℕ tel que g = φ (n₀). Mais alors
n₀ ∈ K ⇔ φ (n₀, n₀) ≠ u,
par définition de K. Or, φ (n₀, n₀) = g (n₀). Donc
φ (n₀, n₀) ≠ u ⇔ g (n₀) ≠ u ⇔ n₀ ∈ ∁_K.
On a ainsi obtenu une contradiction. L’ensemble K est donc récursivement énumérable et non récursif.

La théorie de la récursivité a de nombreux prolongements parmi lesquels figure l’étude des degrés d’indécidabilité, des fonctionnelles récursives de type supérieur, des ensembles admissibles, de la complexité, etc.

B. J.

 H. Rogers, Theory of Recursive Functions and Effective Computability (New York, 1967). / B. Jaulin et J. P. Azra, Récursivité (Gauthier-Villars, 1973).