récursive (fonction) (suite)

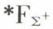Sur les six inclusions qu’il faut prouver, une seule, requiert une démonstration délicate. Il faut en effet, dans ce cas, démontrer que est clos par récurrence. Pour cela, on utilise la fonction β, qui a été introduite par K. Godel et qui a la propriété d’être « densifiante » pour l’ensemble des applications de ℕ dans ℕ, c’est-à-dire qui est telle que, pour toute application f de ℕ dans ℕ et pour tout n ∈ ℕ, il existe n₁, n₂ ∈ ℕ tel que pour tout β (n₁, n₂, x) = f (x). Cette propriété de la fonction β permet de remplacer un quantificateur existentiel portant sur l’ensemble des applications de ℕ dans ℕ par deux quantificateurs existentiels portant sur ℕ dans la formule qui explicite l’opération de récurrence. Cela est possible du fait que la valeur en y d’une fonction f définie par récurrence à partir de deux fonctions g et h ne dépend que des valeurs de f pour x < y. La démonstration des autres inclusions est assez longue, notamment celle qui conduit au résultat Toutefois, certaines de ces démonstrations peuvent être évitées si l’on admet la thèse de A. Church suivant laquelle « toute semi-fonction calculable au sens intuitif est une semi-fonction récursive ». En effet, une semi-fonction calculable par un programme doit être considérée comme une semi-fonction mécaniquement calculable, c’est-à-dire telle qu’il existe un procédé uniforme défini à partir d’un nombre fini de données permettant de passer de la valeur des arguments où cette fonction est définie à la valeur de la fonction après un nombre fini d’étapes.

Ensembles récursifs, récursivement énumérables

Un sous-ensemble de ℕ^p est récursif si sa fonction caractéristique est récursive. Un ensemble est donc récursif si, et seulement si, il existe un procédé de calcul permettant de reconnaître ou de décider si un nombre quelconque appartient ou non à cet ensemble. Un sous-ensemble de ℕ est récursivement énumérable si c’est le domaine de définition d’une semi-fonction récursive. Les énoncés suivants sont équivalents :

• A ⊂ ℕ est récursivement énumérable ;

• A est la projection d’un sous-ensemble récursif de ℕ² ;

• A est l’ensemble des valeurs d’une fonction récursive ;

• A ∈ .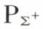

Il existe des ensembles, par exemple X = {n/ il existe x, y, z tel que xⁿ + yⁿ = zⁿ}, dont on sait qu’ils sont récursivement énumérables, mais dont on ignore s’ils sont récursifs. En l’occurrence, si X n’était pas récursif, comme les ensembles finis le sont, cela signifierait que la conjecture de Fermat suivant laquelle X = {1, 2} est fausse ! Toutefois, il existe des ensembles récursivement énumérables qui ne sont pas récursifs. Le problème de la décision en fournit un exemple : l’ensemble des numéros des théorèmes (pour une certaine numérotation admissible de l’ensemble des formules closes du langage de l’arithmétique) de l’arithmétique de Peano du 1^er ordre est récursivement énumérable et non récursif. C’est en ce sens qu’il n’existe pas de procédure mécanique de décision qui, étant donné une formule quelconque de ce langage, permette de reconnaître si cette formule est ou non un théorème de la théorie de Peano. De façon générale, les problèmes de décidabilité ou d’indécidabilité consistent à se poser des questions du type : « Tel ensemble est-il ou non récursif ? »

Exemples.

1. Soit {f₁, f₂, ..., f_n} un ensemble fini de polynômes à coefficients rationnels à n variables. Existe-t-il un algorithme permettant de décider si un polynôme quelconque g de n variables à coefficients rationnels s’écrit sous la forme i = 1 à n étant un polynôme quelconque de n variables ? Modulo une bijection entre l’ensemble des polynômes de n variables à coefficients rationnels et ℕ, un tel problème revient à se demander si un certain sous-ensemble de ℕ est récursif, celui correspondant dans cette bijection à l’idéal engendré par {f₁, f₂, ..., f_n}. En l’occurrence, des résultats de Herman montrent qu’il en est bien ainsi.

2. Existe-t-il un algorithme permettant de décider si un polynôme de n variables à coefficients dans ℤ admet des racines entières ? Ce problème a été formulé par David Hilbert (dixième problème de la fameuse série présentée au Congrès des mathématiciens en 1900) et a été résolu par la négative en 1971 par Y. Mattiaseyvic. La démonstration de ce résultat est essentiellement celle du fait que les ensembles récursivement énumérables sont exactement les ensembles diophantiens, c’est-à-dire les projections dans ℕ^p des ensembles de solutions dans ℕ des polynômes à p + q variables, p, q ∈ ℕ à coefficients dans ℤ. Elle repose sur des résultats antérieurs de Julia Robinson, de Hilary Putnam, de Martin Davis, etc.

3. En démontrant que la théorie des corps finis est décidable, J. Ax a montré notamment qu’il existe un algorithme permettant de décider si un système d’équations diophantiennes est résolubles modulo p pour tous les nombres premiers p.

4. Soit X un ensemble fini et L (X) l’ensemble des suites finies d’éléments de X. Soient (f₁, ..., f_n) et (g₁, ..., g_n) deux éléments de [L (X)ⁿ] et soit ≡ la congruence la plus fine telle que f_i ≡ g_i i = 1 à n. Étant donné deux n-uplets (f₁, ..., f_n) et (g₁, ..., g_n) et un mot h ∈ L (X), existe-t-il un algorithme permettant de décider si h est congru au mot vide pour la congruence associée à ces deux n-uplets ? Ce problème, qui s’appelle le problème des mots pour les monoïdes libres et que l’on peut formuler également dans le contexte des groupes libres, est indécidable. La démonstration de ce type de résultat dans le cas des monoïdes libres s’obtient en utilisant une définition de la récursivité qui fait appel aux machines à chiffres, comme les algorithmes de Markov, les systèmes de Post, les machines de Turing ou bien les grammaires génératives, etc. Dans ce type de machine à programme, on utilise un alphabet fini dont les suites finies d’éléments servent à représenter les nombres. Les instructions que l’on utilise sont explicitées dans les termes de ces symboles ou chiffres et non pas, comme dans la définition donnée, au niveau des nombres. En outre, pour certaines de ces machines, on utilise un seul registre, c’est-à-dire que l’algorithme consiste, à l’aide d’un nombre fini de règles, à transformer un mot sur un alphabet fini.