raisonnement

Opération de la pensée consistant à entraîner des jugements et à en tirer une conclusion.

Raisonnement par récurrence

Ce type de raisonnement utilise un des axiomes de Peano définissant l’ensemble ℕ des entiers naturels et aux termes duquel, si d’une part une propriété dont l’énoncé contient un entier naturel indéterminé n est vraie pour un nombre particulier n₀ ; si d’autre part on peut démontrer, en supposant la propriété vraie pour tout entier p inférieur ou égal à un entier n, que cette propriété est vraie pour n′ = n + 1 ; alors la propriété est vraie pour tout entier n supérieur ou égal à n₀.

Si P(x) signifie : la propriété est vraie pour l’entier x, on a, en résumé,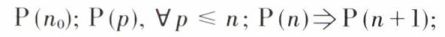

alors P(n), ∀n ∈ ℕ.

Ce raisonnement est très utilisé en mathématique. Très souvent, n₀ = 1, mais il arrive que n₀ > 1. Pour passer de P(n) à P(n + 1), l’hypothèse est P(n) et la conclusion est P(n + 1). Il ne faut pas oublier de vérifier P(n₀), car si on n’a pas P(n₀), c’est-à-dire si on ne trouve pas n₀ tel que P(n₀), on peut très bien démontrer P(n + 1) à partir de P(n) et conclure ainsi à une propriété qui est fausse. Enfin, le raisonnement par récurrence s’impose à l’esprit, car, si P(n) ⇒ P(n + 1), comme P(n₀), alors P(n₀ + 1), puis P(n₀ + 2), ..., et P(n), quel que soit n ∈ ℕ.

Exemples de raisonnements par récurrence

1. Montrer que la somme S_n = 1 + 2 + ... + n des n premiers entiers est égale à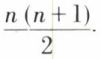
On a à démontrer P(n) :
P(1) : P(1) est vraie.
Supposons que,
Considérons S_n+1 = 1 + 2 + ... + n + (n + 1).
On a d’après l’hypothèse de récurrence.
D’où :

et ainsi P(n + 1) est vraie puisque S_n+1 a même forme que S_p, avec p = n + 1. On a donc bien

On peut se demander d’où vient l’expression de S_n donnée a priori dans cet exemple. On trouve directement la somme S_n en écrivant :
S_n = 1 + 2 + 3 + ... + (n – 1) + n,
puis S_n = n + (n – 1) + ... + 3 + 2 + 1.

On ajoute alors membre à membre ; dans chaque colonne, la somme des deux termes étant égale à n + 1, on trouve :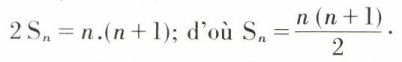

Mais une personne ignorant la forme de S_n et la méthode de calcul direct expliciterait S₂, S₃, S₄, ..., peut-être d’autres sommes encore et chercherait une relation entre le résultat obtenu et le dernier nombre de la somme étudiée. Elle arriverait, peut-être, au résultat explicite À l’aide d’un raisonnement par récurrence, qui s’introduit tout naturellement, elle poserait et chercherait a mettre S_n+1 sous la forme semblable, obtenue à partir de S_n, en remplaçant n par n + 1. C’est ainsi que de nombreux résultats, obtenus sur de petits entiers, peuvent donner naissance à des théorèmes. Mais il faut bien se garder d’annoncer un résultat sans avoir fait complètement la récurrence.

De même, par récurrence, on trouve que la somme des carrés des n premiers entiers est égale à et que la somme des cubes des n premiers entiers est égale à c’est-à-dire au carre de S_n.

2. On considère la fonction numérique Elle est indéfiniment dérivable et on peut calculer

On est tenté de supposer que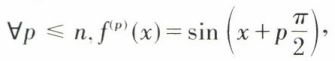

f^(p)(x) désignant la dérivée d’ordre p de f(x). Alors, si on trouve en dérivant une fois de plus :

ou
qui est de la même forme que f⁽ⁿ⁾(x), n étant remplacé par n + 1. Ainsi, pour tout n appartenant à ℕ, si f(x) = sin x, on a

Il existe d’autres exemples de calculs de dérivées d’ordre n, dont la forme est mise en évidence par les premières dérivées et qui sont achevés par un raisonnement par récurrence. Ainsi, la dérivée d’ordre n de la fonction

Raisonnement par l’absurde

Ce type de raisonnement consiste, pour démontrer une proposition Q à partir d’une proposition P, à montrer que 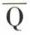, négation de la proposition Q, entraîne , négation de la propriété P, ce qui est une contradiction puisque la proposition P est vraie ou fausse, l’un excluant l’autre. On est donc contraint de conclure à la validité de la proposition Q. On utilise souvent le raisonnement par l’absurde dans la vie courante, sous une forme plus ou moins explicite. Ainsi, le laitier n’est pas encore passé puisque je ne vois pas le bidon de lait à la grille du jardin. Le schéma de ce raisonnement est le suivant : P, le bidon de lait n’est pas à la grille ; Q, le laitier n’est pas passé. En effet, supposer 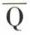, c’est-à-dire le laitier est passé, entraînerait « le lait est à la grille », c’est-à-dire . Mais en mathématique, c’est souvent sous une forme bien abstraite que s’applique le raisonnement par l’absurde.

Exemple de raisonnement par l’absurde

Tout sous-groupe d’un groupe cyclique est cyclique. Si G = {e, a, a², ..., a^n–1} est un groupe cyclique et H un sous-groupe de G, le sous-groupe H ⊂ G est formé d’éléments de G, donc de la forme a^r, r ∈ ℕ, Soit p le plus petit des exposants r des éléments de H ; p existe, car le sous-groupe H est fini, puisque le groupe G est fini. Le groupe (a^p) engendré par a^p, c’est-à-dire formé des éléments de la forme (a^p)^m, m ∈ ℕ, est inclus dans le sous-groupe H, puisque celui-ci doit contenir toutes les puissances de a^p, car a^p ∈ H. Supposons que le sous-groupe H soit distinct de (a^p). Alors il existe dans le sous-groupe H un élément qui n’est pas de la forme a^mp ; soit a^r cet élément. Comme p ne divise par r, les nombres entiers p et r ont un plus grand diviseur commun, d, inférieur à r et à p et il existe deux entiers relatifs, u et v, tels que pu + rv = d (identité de Bézout). On en déduit que (a^p)^u (a^r)^v = a^pu+rv = a^d ∈ H, car a^p ∈ H et a^r ∈ H, d’où l’existence dans le sous-groupe H d’un élément a^d avec d < p. Ce qui contredit la propriété de p et est donc impossible. Il n’existe aucun élément du sous-groupe H qui ne soit de la forme (a^p)^m, et H = (a^p), qui est cyclique puisque engendré par a^p et fini.