ℝ (suite)

On peut alors définir les éléments positifs qui forment l’ensemble ℝ₊ ainsi que l’ensemble – ℝ₊ des éléments négatifs tels que :
x et y ∈ ℝ₊ ⇒ x + y ∈ ℝ₊ ;
x et y ∈ ℝ₊ ⇒ xy ∈ ℝ₊ ;
ℝ₊ ⋂ – ℝ₊ = {0} ; ℝ₊ ∪ – ℝ₊ = ℝ.

On a la règle des signes :
(x et y ∈ ℝ₊ ou x et y ∈ – ℝ₊) ⇒ xy ∈ ℝ₊
(x ∈ ℝ₊ et y ∈ – ℝ₊) ⇒ xy ∈ – ℝ₊.

On définit une valeur absolue, notée par une double barre verticale :
|x| = x, si x ∈ ℝ₊ ; |x| = – x, x ∈ – ℝ₊ ; ainsi, |0| = 0.
Cette valeur absolue satisfait l’inégalité triangulaire

2. Le corps ℝ est complet.

Toute suite de Cauchy d’éléments du corps ℝ est convergente dans ce corps, c’est-à-dire a une limite dans ℝ. Une suite d’éléments du corps ℝ, (x_m), est dite « de Cauchy » si, pour tout réel ε > 0, il existe un entier n₀ = n(ε) tel que, pour tous indices n et m supérieurs à n₀, on a |x_n – x_m| < ε. Il existe des suites de Cauchy d’éléments rationnels qui ne convergent pas dans le corps ℚ des nombres rationnels ; mais ces suites convergent dans le corps ℝ, qui possède la propriété plus forte d’être complet.

3. Le corps ℚ des rationnels est dense dans ℝ, ce qui signifie qu’entre deux nombres réels quelconques il existe toujours un rationnel. De plus, entre deux nombres rationnels quelconques, il y a toujours un nombre irrationnel.

4. Le corps ℝ est archimédien : pour tout élément x réel strictement positif et pour tout élément a réel positif, il existe un entier naturel n tel que

Approximation décimale d’un nombre réel

D’après l’axiome d’Archimède, étant donné le nombre réel x et un entier naturel n quelconque, le nombre réel 10ⁿ x est compris, au sens large, entre deux entiers consécutifs, a_n et a_n + 1. Par suite,

Le nombre décimal
est la valeur décimale approchée par défaut du nombre x, à 10^–n près, (a_n + 1)10^–n étant la valeur approchée par excès. Si le nombre n augmente, on obtient deux suites,

qui sont adjacentes, car 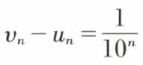tend vers zéro quand n → + ∞ ; d’autre part, en comparant avec x,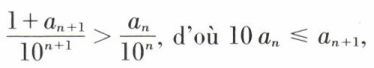

ce qui entraîne de même, d’où, 10(1 + a_n) > a_n+1, ou d’où

Les suites u_n et v_n ont même limite, supérieure à toutes les quantités u_n et inférieure à toutes les quantités v_n : cette limite est le nombre réel x.

Interprétation géométrique des nombres réels

Les nombres réels peuvent être représentés par les points d’un axe de façon que, ayant choisi sur une droite une origine O et un vecteur unité d’origine O et d’extrémité U, à chaque nombre réel corresponde un point et un seul et réciproquement tout point soit associé à un réel unique.

Les axiomes de la droite euclidienne qui permettent de définir cette correspondance biunivoque sont :
1^o L’axiome d’Archimède, aux termes duquel, étant donné un point M quelconque de x′x, on peut trouver un entier n tel que n . OU > OM ;
2^o L’axiome de Cantor-Dedekind, aux termes duquel les segments A₁B₁, A₂B₂, ..., A_nB_n, ..., dont chacun contient le suivant et dont la largeur tend vers zéro, le nombre des segments augmentant indéfiniment, ont en commun un point et un seul (segments emboîtés). Étant donné un nombre réel x, on peut le définir par deux suites adjacentes de valeurs décimales approchées qui sont représentées sur un axe par des segments emboîtés, d’où un point I correspondant à ce nombre réel x. Inversement, étant donné un point M sur l’axe x′x, il existe p ∈ ℤ tel que 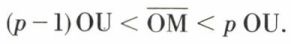En divisant l’unité OU en 10ⁿ parties égales, il existe un entier a_n unique tel que d’où deux suites adjacentes définissant un nombre réel x qui est l’abscisse de M sur x′x.

Propriétés des sous-ensembles de ℝ

Théorème de la borne supérieure

Toute partie P du corps ℝ des nombres réels, majorée (minorée) et non vide, possède une borne supérieure (inférieure) dans ℝ.

Soit b₀ un majorant de la partie P et a₀ un élément quelconque de cette partie ; on considère le milieu c₀ de [a₀, b₀]. Si [c₀, b₀] contient des éléments de P, on recommence en posant [a₁, b₁] = [c₀, b₀]. Sinon, c₀ est un majorant de P et on pose a₁ = a₀, b₁ = c₀. Ce procédé (par dichotomie) se poursuit et on obtient une suite d’intervalles [a_m, b_m], de largeur qui tend vers zéro quand m → + ∞. Pour toute valeur m, la quantité b_m majore P et P ⋂ [a_m, b_m] est non vide. L’axiome de Cantor-Dedekind s’applique aux segments emboîtés ainsi définis qui ont en commun un point et un seul définissant un nombre réel l qui majore P comme toutes les quantités b_m, qui tendent d’ailleurs vers la limite l. Tout intervalle ]l – ε, l + ε[ contient au moins un élément de la partie P puisqu’il contient [a_m, b_m] pour une valeur de m assez grande. On dit que la limite l est adhérente à P : l est la borne supérieure de P ou plus petit majorant.

Topologie de la droite réelle

Les intervalles du corps ℝ, [a, b], ]a, b], [a, b[ ou ]a, b[, désignent respectivement l’ensemble des réels x tels que

l’intervalle est fermé, semi-ouvert ou ouvert. Un sous-ensemble A de ℝ est un ouvert s’il est vide ou si pour toute valeur x de A il existe un intervalle ouvert de centre x contenu dans A. La droite ℝ et l’ensemble vide, Ø, sont des ouverts. Toute intersection finie d’ouverts est un ouvert. Toute réunion d’ouverts est un ouvert. Tout intervalle ouvert est un ouvert. Un sous-ensemble B de ℝ est fermé si son complémentaire dans ℝ est ouvert. Un voisinage d’un point x de ℝ est un sous-ensemble contenant un ouvert contenant x. Le point x₀ de ℝ est un point d’accumulation pour une partie A de ℝ si tout voisinage de x₀ contient un point du sous-ensemble A distinct de x₀. Un sous-ensemble A de ℝ est fermé si, et seulement si, il contient ses points d’accumulation.

• Théorème de Bolzano- Weierstrass. Toute partie P bornée de ℝ comportant une infinité d’éléments a au moins un point d’accumulation.

• Théorème de Borel-Lebesque. De tout recouvrement ouvert d’un intervalle fermé borné [a, b], on peut extraire un sous-recouvrement fini.

Ce théorème signifie que, s’il existe un recouvrement de [a, b] par une famille d’ouverts (w_i)_i ∈ I, l’ensemble I étant infini, on peut trouver un ensemble fini J ⊂ I tel que la famille (w_i)_i ∈ J recouvre l’intervalle [a, b].