quadrique (suite)

La classification complète précédente fait apparaître, comme cas particuliers, des quadriques dégénérées, que l’on peut être surpris de trouver, comme deux plans sécants par exemple. Cela provient de la définition d’une quadrique par une équation du second degré. Ainsi, l’équation x² – y² = 0 est celle d’une quadrique dégénérée en deux plans passant par l’axe Oz, l’un d’équation x – y = 0, l’autre d’équation x + y = 0. D’ailleurs, on peut étudier la dégénérescence d’une quadrique, indépendamment de la réalité de ses points à l’infini, au moyen des points doubles éventuels de cette quadrique, et l’on aboutit à une classification en espèces. La dénomination de quadrique est alors réservée aux quadriques de première espèce, c’est-à-dire aux ellipsoïdes, aux hyperboloïdes et aux paraboloïdes hyperboliques ou elliptiques, quadriques n’ayant aucun point double.

Classification en espèces au moyen des points doubles

Un point P(X₀, Y₀, Z₀, T₀) est double sur la quadrique (S) d’équation homogène F(X, Y, Z, T) = 0 ou d’équation cartésienne f(x, y, z) = F(x, y, z, 1) si, quel que soit le point P′, n’appartenant pas à (S), la droite PP′ coupe (S) en deux points confondus avec P. Pour qu’il en soit ainsi, il faut et il suffit que

où 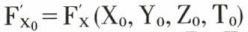est la dérivée partielle de F(X, Y, Z, T) par rapport à X au point P(X₀, Y₀, Z₀, T₀), ayant des significations analogues. Le système (1) s’écrit :

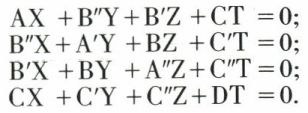
Le déterminant de ce système est celui de la forme quadratique F(X, Y, Z, T) ou de la matrice

telle que :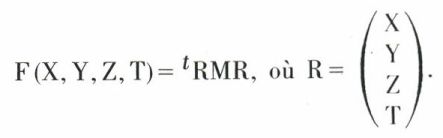

• Si dét M ≠ 0, le système (1) n’a pas d’autre solution que la solution banale X = Y = Z = T = 0 ; la quadrique (S) n’a pas de point double ; elle est de première espèce.

• Si dét M = 0 et si son rang est trois, les quatre plans dont les équations constituent le système (1) ont un point commun et un seul ; la quadrique (S) a un point double ; elle est de seconde espèce, c’est un cône ou un cylindre.

Si dét M = 0 et si son rang est deux (il existe au moins un déterminant d’ordre deux, extrait de la matrice M, non nul), les plans représentés par les équations (1) ont une droite en commun ; la quadrique (S) a une droite de points doubles et est décomposée en deux plans distincts ; elle est de troisième espèce.

• Si dét M = 0 et si son rang est un (tous les déterminants d’ordre trois ou deux extraits de la matrice M sont nuls), les quatre équations du système (1) se réduisent à une seule, qui est l’équation d’un plan ; la quadrique (S) se réduit à un plan double (deux plans confondus), qui est un plan de points doubles ; elle est de quatrième espèce.

Les deux classifications complètes précédentes peuvent être utilisées dans tous les cas où l’on étudie une quadrique d’équation donnée. La recherche des points doubles éventuels revient en effet au calcul de déterminants d’ordres inférieurs ou égaux à quatre. La recherche des points à l’infini revient à l’étude d’un cône (C) d’équation φ(X, Y, Z) = 0, qui, à son tour, est une quadrique. On peut donc chercher si ce cône n’admet qu’un point double, l’origine, ou s’il admet une droite ou un plan de points doubles, ce qui fournit le genre de la quadrique (S). En effet, si le cône (C) est décomposé, il est facile de voir si la décomposition donne deux plans réels ou imaginaires. Dans le cas où le cône (C) n’est pas décomposé, on décèle si (C) est réel ou imaginaire en cherchant des points réels sur (C) en dehors de l’origine, ce que l’on peut faire en coupant le cône (C) par des plans appropriés. On arrive ainsi à identifier la quadrique (S). Mais il faut, pour chacune des catégories de quadriques citées, donner les propriétés caractéristiques, ce qui peut se faire par l’étude des équations réduites des quadriques, équations auxquelles on peut toujours arriver par des changements d’axes de coordonnées convenables. On peut procéder à cette recherche en axes quelconques, mais il est préférable de se placer dans une base orthonormée et de ne faire des changements d’axes qui ne conduisent qu’à des repères eux-mêmes orthonormés. On arrive ainsi à une classification complète qui met en évidence le genre et l’espèce de la quadrique, et qui montre en quelque sorte cette quadrique.

Classification par réduction de l’équation en axes orthonormés

Le centre d’une quadrique (S) est le centre de symétrie de cette quadrique, c’est-à-dire le point I à distance finie tel que toute droite passant par I coupe la quadrique (S) en deux points P et P′ symétriques par rapport à I. Pour que I (x₀, y₀, z₀) soit un centre, il faut et il suffit que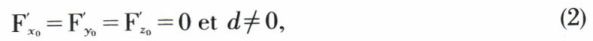

d étant le cofacteur de D dans dét M, c’est-à-dire le déterminant de la matrice M₁ associée à la forme quadratique φ(X, Y, Z).

Réduction des quadriques à centre

On prend comme nouvelle origine le centre I (x₀, y₀, z₀) de la quadrique (S) ; les formules de changement d’axe sont
x = x′ + x₀, y = y′ + y₀, z = z′ + z₀ ;
on obtient l’équation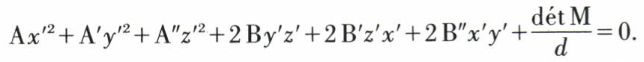

On détermine ensuite les valeurs propres de la matrice

racines de l’équation caractéristique de M₁ :

La matrice M₁ étant symétrique réelle a trois valeurs propres réelles (non nulles, puisque le produit de ces valeurs propres est égal à d ≠ 0), et il existe toujours une base de vecteurs propres qui, rapportés à une base orthonormée (ce qui est le cas) sont deux à deux orthogonaux. On peut donc normer ces vecteurs de façon à obtenir une base orthonormée 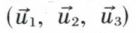correspondant aux valeurs propres λ₁, λ₂, λ₃ de la matrice M₁. Dans cette nouvelle base (d’origine I), l’équation réduite de (S) est

En posant, si dét M ≠ 0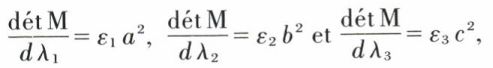

avec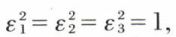
les quantités ε_i étant choisies convenablement suivant les signes des valeurs propres λ₁, λ₂ et λ₃, on arrive aux différentes équations réduites des quadriques à centre.

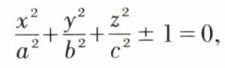•  ellipsoïde, réel si l’on a – 1 et imaginaire si l’on a + 1.

•  hyperboloïde à une nappe, ou H₁.

•  hyperboloïde à deux nappes, ou H₂.