polarisation de la lumière (suite)

Équation de propagation

L’élimination de entre les équations de Maxwell rappelées ci-dessus nous conduit à l’équation de propagation

Étant donné que et ne sont pas, dans le cas général, colinéaires, n’est pas nul, alors qu’il l’est dans le cas d’un milieu isotrope.

Dans le cas d’une onde plane polarisée rectilignement, la résolution de l’équation (1) conduit à une relation entre les vecteurs , et (vecteur unitaire normal à l’onde) et la vitesse v de propagation, qui peut se mettre sous la forme

Cette relation montre que la vitesse de propagation (donc l’indice du milieu) dépend de la direction normale à l’onde et de la direction des champs. Elle est, par contre, indépendante du module de ces champs.

Structure de l’onde plane se propageant dans un milieu anisotrope

L’étude des équations de Maxwell et de l’équation (2) montre, d’une part, que et sont perpendiculaires entre eux ainsi qu’au vecteur normal , et d’autre part, que , et sont coplanaires. De plus, le vecteur de Pointing définit la direction de propagation de l’énergie, c’est-à-dire la direction du rayon lumineux, qui est donc orthogonal à et à et non, comme dans le cas des milieux isotropes, confondu avec la normale à l’onde (fig. 3). Il faut aussi remarquer que les vecteurs , et vibrent en phase.

Étude de la propagation d’ondes planes polarisées rectilignement

Cette étude se fait à l’aide de l’équation (2) déduite de l’équation de propagation, de l’équation qui traduit l’équation et enfin de l’équation

Ces trois équations, dont deux sont vectorielles, fournissent donc sept équations comportant neuf inconnues, à savoir les trois composantes de , les trois composantes de , deux composantes de (puisqu’il est unitaire) et la vitesse v. On voit donc que, si l’on se donne la direction d’un vecteur, soit par exemple celle de ou celle de , le problème de la propagation d’une onde plane sera possible à résoudre. On va, dans la suite, étudier ces deux cas : on se donnera la direction de polarisation et l’on cherchera quelles sont alors la direction et la vitesse de propagation possibles, ou bien on se donnera la direction de propagation et l’on cherchera quelles sont alors les directions de polarisation et les vitesses possibles.

• Propagation d’une onde plane de direction de polarisation donnée. L’élimination du vecteur entre les équations ci-dessus conduit à la relation suivante :

où v₁, v₂ et v₃ sont les vitesses principales définies plus haut, et p, q et r les cosinus directeurs du vecteur . On voit donc que, pour une direction de polarisation donnée, il existe deux vitesses + v et – v possibles. On pourrait obtenir une équation analogue permettant de calculer l’indice 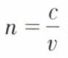en fonction des indices principaux n₁, n₂ et n₃, qui est :

On obtient une représentation graphique de ces résultats en faisant intervenir l’ellipsoïde des indices. En effet, si, à partir d’un point O quelconque du milieu, on mène un vecteur parallèle à et tel que le module de soit égal à l’indice n, les coordonnées de M sont x = pn, y = qn et z = rn dans un repère orthonormé d’origine O. L’équation (4), dans laquelle on remplace pn, qn et rn par x, y et z respectivement, devient l’équation d’une surface appelée ellipsoïde des indices :

On montre alors que la normale au point M à cet ellipsoïde est parallèle au champ  ; or, on sait, après l’étude de la structure de l’onde, que le vecteur normal est perpendiculaire à et qu’il est dans le plan Il n’y a donc qu’une direction de propagation possible pour une onde plane de direction de polarisation donnée.

Si et sont colinéaires, c’est-à-dire parallèles à un des axes principaux, toute direction perpendiculaire à celle de ces vecteurs est une direction de propagation possible.

• Propagation d’une onde plane de direction de propagation donnée. Il faut, dans ce cas, déterminer les vitesses de propagation possibles ainsi que les directions de propagation. En éliminant les composantes de dans le système d’équations précédent, on est conduit à l’équation suivante :

α, β et γ étant les cosinus directeurs du vecteur normal . Cette équation est appelée équation de Fresnel. On peut l’écrire en faisant intervenir les indices ; elle devient

L’équation (5) est une équation du second degré en v², et l’on montre facilement qu’elle admet toujours deux racines réelles et positives v′² et v″² ; les vitesses possibles sont donc ± v′ et ± v″ (les signes ± indiquant que les deux sens de propagation sont possibles). Il peut donc y avoir propagation d’ondes planes polarisées rectilignement dans toutes les directions. Pour une direction de propagation normale donnée, seules deux vitesses de propagation dans un sens sont possibles. Il reste à déterminer la direction de polarisation de ces vibrations, qui se propagent sans déformation. On montre que, étant donné une direction de propagation, il n’y a dans le plan d’onde correspondant que deux directions de polarisation, orthogonales entre elles, qui se propagent sans déformation, l’une avec la vitesse v′, l’autre avec la vitesse v″, v′ et v″ étant solutions de l’équation de Fresnel.

En effet, si l’on considère l’ellipsoïde des indices (fig. 4), le plan d’onde coupe cet ellipsoïde suivant une ellipse. Le vecteur , normal à , est dans le plan d’onde ; il doit donc être tangent à cette ellipse et, de plus, perpendiculaire à , c’est-à-dire au rayon vecteur du point courant de l’ellipse. La seule possibilité d’avoir cette configuration est que soit dirigé suivant l’un des axes de l’ellipse, d’où les deux indices ou les deux vitesses possibles. Si la conique d’intersection de l’ellipsoïde des indices et du plan d’onde est un cercle, toutes les directions de polarisation sont possibles dans ce plan, l’indice étant égal au rayon du cercle. Il est facile de voir que, dans le cas d’un milieu uniaxe (ellipsoïde de révolution, puisque n₁ = n₂ = n₀), l’une des directions est la projection de l’axe de révolution sur le plan d’onde ; c’est la vibration extraordinaire ; l’autre est orthogonale à l’axe : c’est la vibration ordinaire. On peut représenter graphiquement ces résultats en faisant intervenir une surface appelée surface des indices. En effet, si l’on considère un vecteur (O étant un point quelconque du milieu) parallèle au vecteur normal et tel que le module de ce vecteur soit égal à l’indice n, c’est-à-dire tel que les coordonnées de M sont x = αn, y = βn et z = γn. En éliminant n entre ces relations et l’équation de Fresnel, on trouve que le lieu de M est une surface du quatrième ordre, représentée sur la figure 5 dans le cas d’un milieu biaxe et sur la figure 6 dans le cas d’un milieu uniaxe. La représentation est faite dans la région où x, y et z sont positifs ; la surface complète est symétrique par rapport aux différents plans de coordonnées ; on voit que, dans le cas des milieux biaxes, on aura quatre points coniques tels que I. Les deux vibrations pourront se propager suivant les directions OI avec la même vitesse. Les axes tels que OI sont appelés axes du milieu, d’où le nom de milieu biaxe. Dans le cas des milieux uniaxes, c’est-à-dire tels que n₁ = n₂ = n₀ et n₃ = n_e, la surface des indices est de révolution et comprend une nappe sphérique de rayon n₀ et une nappe ellipsoïdale ; si n_e < n₀, le milieu est dit « négatif » (c’est le cas du spath), si n_e > n₀, le milieu est dit « positif » (c’est le cas du quartz).