continu
MATHÉMATIQUES
Hypothèse du continu
Elle désigne la conjecture selon laquelle il n'existe pas d'ensemble qui ait une puissance intermédiaire entre ℵ0 (cardinal des ensembles dénombrables) et la puissance du continu. En un sens, on peut aujourd'hui considérer que le problème a été résolu, d'abord par Gödel, qui a montré en 1938 la consistance de l'hypothèse du continu avec les autres axiomes de la théorie ZF des ensembles, puis par P. Cohen, qui a montré l'indépendance de cette hypothèse (1963) : que l'on adjoigne l'hypothèse du continu ou sa négation aux axiomes de la théorie ZF, aucune contradiction n'en découlera.
Puissance du continu
Cardinal, noté ℵ1, de l'ensemble des nombres réels, c'est aussi celui du segment [0,1] et de l'espace réel ℝ2.
Fonction f continue en un point x0
On la définira sous différentes formes suivant que l'on se trouve dans des espaces topologiques, métriques ou plus simplement dans ℝ muni de sa métrique habituelle.
(1) Si f est une application de E1 dans E2 (E1 et E2 espaces topologiques), f est continue en x0 si tout voisinage de f(x0) a pour image par f−1 un voisinage de x0.
(2) Si f est une application de (E1, d1) dans (E2, d2) [E1 et E2 espaces métriques], f est continue en x0 si
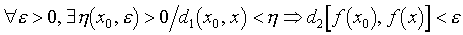
(3) Si f est une application de ℝ dans ℝ, f est continue en x0 si
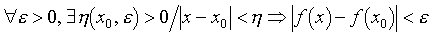 .
.
Dans les cas (2) et (3), la continuité est dite uniforme lorsque l'élément η de la définition ne dépend plus de x0, mais seulement du choix de ε. Dans le cas (3), la notion de continuité est liée à celle du trait de la représentation graphique au point d'abscisse x0.



