optique géométrique (suite)

Postulats fondamentaux

Propagation rectiligne de la lumière

Dans un milieu homogène et isotrope, l’indice est le même en chaque point du milieu. Pour que l’équation (2) soit vérifiée, quel que soit on doit avoir qui s’écrit dans le cas considéré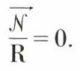

Le rayon de courbure de la trajectoire est infini ; la trajectoire est une droite. Lorsqu’un système est formé d’une succession de milieux homogènes séparés par des dioptres, la propagation est une ligne brisée (fig. 4) composée de segments de droites.

Principe du retour inverse

Dans une expérience bien définie, calculons les chemins optiques (AB) et (BA). Entre ces deux calculs, chaque élément est changé de signe ; on inverse les bornes. Les intégrales ont même valeur, et les courbes extrémales sont les mêmes. La lumière suit un chemin identique, qu’elle progresse de A vers B ou de B vers A.

Lois de Descartes

Ces relations indiquent comment sont déviés les rayons lumineux à la traversée d’un dioptre qui sépare deux milieux d’indice de réfraction n₁ et n₃ (fig. 5).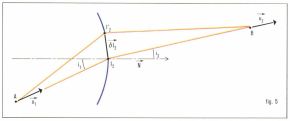

Le chemin suivi par la lumière est AI₂B ; (AB) = n₁(AI₂) + n₃(I₂B). Le point I′₂, voisin de I₂ sur le dioptre, définit un chemin voisin du précédent. D’après le principe de Fermat,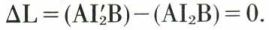

ΔL, calculé d’après l’expression (1), s’écri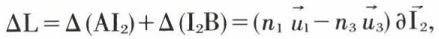t

et 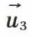étant les vecteurs unitaires portés par AI₂ et I₂B.

Le vecteur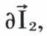 qui joint deux points voisins I₂ et situés sur le dioptre, est dans le plan tangent au dioptre. Le principe de Fermat indique que

Les vecteurs 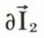et sont orthogonaux ou, ce qui est équivalent,

Les vecteurs , 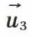et 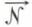(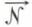, vecteur unitaire de la normale au dioptre) sont coplanaires. C’est la première loi de Descartes : le rayon réfracté est dans le plan d’incidence, plan déterminé par le rayon incident et la normale au dioptre. En multipliant scalairement par 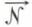l’équation (3), on déduit la valeur de K et l’expression vectorielle de la loi de Descartes, où i₁ et i₃ sont les angles d’incidence et de réfraction :

En multipliant les deux membres de l’équation (3) par le vecteur unitaire de la tangente, on obtient la relation de Descartes n₁ sin i₁ = n₃ sin i₃.

En écrivant que n₁ = 1 et que n₃ = – 1, on obtient les lois de Descartes relatives à la réflexion :
1. le rayon réfléchi est dans le plan d’incidence ;
2. les angles d’incidence et de réflexion ont même valeur absolue et sont de signes contraires.

L’expression vectorielle est (fig. 6), 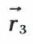étant le vecteur unitaire du rayon réfléchi.

Théorème de Malus

a) La surface d’onde est l’ensemble des points obtenus en portant sur chaque trajectoire issue d’une source S un même chemin optique.
b) Selon le théorème, les surfaces d’onde sont normales aux rayons lumineux.

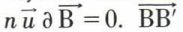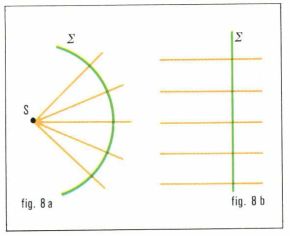
On construit une surface d’onde Σ en portant sur chacune des trajectoires issues de S des chemins optiques égaux de valeur L. La variation du chemin optique des deux rayons voisins SB et SB′ est nulle. D’après l’équation (1), ΔL a pour expression est situé dans le plan tangent à la surface d’onde. Le produit scalaire les rayons sont normaux aux surfaces d’onde (fig. 7). En milieu homogène, la surface d’onde relative à une source ponctuelle est une sphère (fig. 8a). Lorsque la source est à l’infini, les rayons sont parallèles et la surface d’onde est un plan (fig. 8b).

Propagation dans un milieu non homogène

Le milieu présente une variation continue de l’indice de réfraction et nous nous limitons au cas où la répartition possède un plan de symétrie pris pour plan de figure. La condition d’extrémale s’écrit

En multipliant scalairement les deux nombres par ,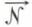

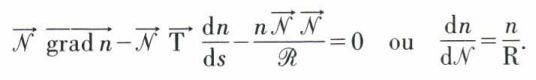
Les rayons ne se propagent plus en ligne droite, mais présentent une courbure

Les phénomènes de mirage, la réfraction atmosphérique trouvent là leur explication (fig. 9 et 10).

Formation des images en optique géométrique

Stigmatisme rigoureux

À partir de ces lois simples, on montre que certains instruments forment des images parfaites. L’image A′ du point A de l’axe d’un instrument de révolution est parfaite lorsque tous les rayons issus de A passent par A′ (fig. 11). Les milieux sont homogènes, les surfaces d’onde objet Σ et image Σ′ sont des sphères. La condition pour qu’un système soit rigoureusement stigmatique est que le chemin optique (AA′) garde une valeur constante quel que soit le rayon choisi. Le miroir parabolique est un exemple de tels systèmes (fig. 12). Pour que le stigmatisme soit conservé pour un point objet B situé dans le plan perpendiculaire à l’axe passant par A, on doit vérifier la relation d’Abbe
ny sin α = n′y′ sin α′ ;
y et y′ désignent la grandeur de l’objet AB et de l’image A′B′ ; α et α′ sont les angles d’ouverture objet et image des systèmes optiques. C’est la relation d’Herschell qui fixe les conditions pour qu’un couple de points de l’axe C et C′ voisins de A et de A′ soit encore stigmatique. Ces deux relations sont incompatibles. L’instrument d’optique stigmatique dans un volume est irréalisable.

Le choix de la relation à vérifier est déterminé en fonction des conditions d’utilisation de l’appareil à construire. La relation d’Herschell est utile pour un instrument destiné à viser un point mobile sur l’axe ; la relation d’Abbe doit être vérifiée pour un système destiné à former l’image d’un objet plan perpendiculaire à l’axe.