métamathématique (suite)

Remarque

Par un abus de langage commode, la complétude de la logique des propositions (v. calcul des propositions) et l’incomplétude de celle des prédicats aux sens forts (v. calcul des prédicats) ont été énoncées sur des systèmes qui contenaient des schémas d’axiomes.

La complétude sémantique, ou complétude au sens faible, sera définie plus bas.

Enfin, 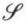est décidable s’il existe une procédure réglée qui permet, en un nombre fini d’étapes, de répondre par oui ou par non à la question : l’expression bien formée A est-elle un théorème de  ?

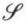Remarque

Par définition, l’alphabet d’un système formel, l’ensemble de ses expressions bien formées, celui de ses axiomes et celui de ses règles de transformation sont décidables. Le problème de la décision (anglais decision problem, allemand Entscheidungsproblem) ne concerne donc que l’ensemble des théorèmes.

Rôle privilégié de l’arithmétique

La notion de système formel est définie de telle sorte que tous les ensembles qui y figurent sont finis ou dénombrables. Il est donc possible d’énumérer tous les éléments d’un système formel : les signes de l’alphabet, les expressions bien formées et les suites d’expressions qui constituent une preuve de l’une d’elles. On pourra donc attribuer une étiquette numérique à chaque élément d’un système formel, son nombre de Gödel. Il suffit pour cela d’imaginer un procédé tel que, étant donné un entier naturel n quelconque, on puisse décider s’il est nombre de Gödel d’un élément du système et, si oui, duquel.

Une telle arithmétisation des systèmes formels a une importance fondamentale. Au lieu de parler, disons, de l’expression A, on pourra parler de son nombre de Gödel, un peu comme l’hôtelier qui monte le journal au 27, au lieu de le remettre au client de la chambre 27. Mais ici les choses vont plus loin. Les propriétés des éléments d’un système formel, les relations qu’ils soutiennent entre eux s’exprimeront comme des propriétés et des relations numériques. On pourra en conséquence étudier les systèmes formels en utilisant le langage de l’arithmétique. Quant à la rigueur souhaitable, on l’obtiendra en construisant un système formel susceptible d’être interprété en termes arithmétiques. Il suffit pour cela d’élargir convenablement la logique des prédicats du 1^er ordre avec identité (v. calcul des prédicats).

Introduisons d’abord un terme constant O (lu « zéro ») et un opérateur unaire ′ (lu « le suivant de »). Les termes (les nombres formels) seront définis inductivement, de sorte que O, O′, O″, Ot′... sont des nombres formels qui correspondent respectivement à 0, 1, 2, 3... Si n est un nombre intuitif, par exemple 3, nous noterons n le nombre formel correspondant, soit Ot′. Introduisons ensuite deux opérateurs binaires + et . , tels que si n et m sont des nombres formels, n + m et n . m en soient aussi. Cela fait, on posera que les variables d’objets x, y... prennent leurs valeurs sur l’ensemble des nombres formels. Il ne reste plus qu’à postuler des axiomes, en plus de ceux du calcul des prédicats, pour fixer le sens des constantes O, ′, +, et .
(α 1) un schéma, qui représente donc une infinité d’axiomes et que l’on appelle souvent le principe d’induction (5^e axiome de Giuseppe Peano [1858-1932]) :
A(O) ∧ (∀x)
(A(x) ⊃ A(x′) . ⊃ A(y)) ;
(α 2) ~ (n′ = O) soit O n’a pas de prédécesseur (3^e axiome de Peano) ;
(α 3) n′ = m′ · ⊃ · n = m soit un nombre n’a qu’un prédécesseur (4^e axiome de Peano).

Remarque

Les deux premiers axiomes de Peano sont inclus dans la définition inductive des nombres formels.
qui définissent inductivement l’addition
qui définissent inductivement la multiplication.

Dès lors, si l’on veut dire, par exemple, que « n est pair » ou que « n est inférieur ou égal à m », on pourra écrire :
(∃x)(~(x = O) ∧ O″ . x = n),
(∃x)(x + m = n),
et des écritures analogues pour exprimer des propriétés et des relations plus complexes.

Calculabilité

Il s’agit en somme d’une généralisation du problème de la décision. Par l’intermédiaire de l’arithmétisation, en effet, ce problème peut se ramener à se demander si une fonction d’entiers est effectivement calculable ou non. Cela revient à répondre à la question suivante : étant donné une fonction arithmétique f(x₁, ..., x_n) et une assignation de valeurs entières aux x_j, peut-on calculer la valeur de f ? La réponse dépend naturellement des moyens de calcul dont on dispose. Ainsi, pour prendre un exemple caricatural, on ne pourra calculer la valeur de la fonction f(x) = x + 10⁶ si l’on ne dispose pas d’un compteur de plus de cinq chiffres. Les logiciens se sont donc attachés à définir, indépendamment de toutes considérations concrètes, des classes de fonctions, aussi larges que possible, et dont ils pouvaient s’assurer qu’elles étaient théoriquement calculables. Il en existe trois principales.
1. La classe des fonctions définie par A. Church (né en 1903) et S. C. Kleene (né en 1909) dans les années 1932 à 1935 par le biais du calcul de la λ-conversion. Il s’agit là d’un formalisme qui s’apparente à la logique combinatoire (v. logique combinatoire).
2. La classe des fonctions dites récursives générales, introduite par Gödel en 1934. On l’obtient à partir de trois familles de fonctions : la fonction successeur f(x) = x′,
les fonctions constantes
f(x₁, ..., x_n) = k,
les fonctions projections
f(x₁, ..., x_n) = x_i,
et par trois groupes d’opérateurs : opérateurs de composition, de récurrence et de minimisation. Si l’on ne fait usage que des deux premières familles d’opérateurs, on obtient ce que l’on appelle les fonctions récursives primitives.
3. Les fonctions calculables par une machine théorique, dite machine de Turing et décrite en 1936-37 par A. M. Turing (1912-1954). Il s’agit là d’une machine qui analyse l’idée de calcul en opérations tout à fait élémentaires : lire un symbole, le conserver, l’effacer, le remplacer par un autre, etc.

Comme on a pu démontrer que ces trois classes de fonctions étaient équivalentes, Church a émis en 1936 la thèse qui porte son nom et qui postule que ces classes coïncident avec celle que l’on considère intuitivement comme comprenant les fonctions effectivement calculables.